31. The sum of $$\frac{3}{{1 \cdot 2}} \cdot \frac{1}{2} + \frac{4}{{2 \cdot 3}} \cdot {\left( {\frac{1}{2}} \right)^2} + \frac{5}{{3 \cdot 4}} \cdot {\left( {\frac{1}{2}} \right)^3} + ......\,{\text{to }}n$$ terms is equal to
A
$$1 - \frac{1}{{\left( {n + 1} \right){2^n}}}$$
B
$$1 - \frac{1}{{n \cdot {2^{n - 1}}}}$$
C
$$1 + \frac{1}{{\left( {n + 1} \right){2^n}}}$$
D
None of these
Answer :
$$1 - \frac{1}{{\left( {n + 1} \right){2^n}}}$$
32. The sum of the first $$n$$ terms of the series $${1^2} + {2.2^2} + {3^2} + {2.4^2} + {5^2} + {2.6^2} + ....{\text{ is }}\frac{{n{{\left( {n + 1} \right)}^2}}}{2}$$ when $$n$$ is even. When $$n$$ is odd the sum is
A
$${\left[ {\frac{{n\left( {n + 1} \right)}}{2}} \right]^2}$$
B
$$\frac{{{n^2}\left( {n + 1} \right)}}{2}$$
C
$$\frac{{n{{\left( {n + 1} \right)}^2}}}{4}$$
D
$$\frac{{3n\left( {n + 1} \right)}}{2}$$
Answer :
$$\frac{{{n^2}\left( {n + 1} \right)}}{2}$$
33. If $$\left( {2n + r} \right)r,n \in N,r \in N$$ is expressed as the sum of $$k$$ consecutive odd natural numbers then $$k$$ is equal to
A
$$r$$
B
$$n$$
C
$$r + 1$$
D
$$n + 1$$
Answer :
$$r$$
34. If $${\log _{10}}2,{\log _{10}}\left( {{2^x} - 1} \right)$$ and $${\log _{10}}\left( {{2^x} + 3} \right)$$ are three consecutive terms of an A.P, then the value of $$x$$ is
A
$$1$$
B
$${\log _{5}}2$$
C
$${\log _{2}}5$$
D
$${\log _{10}}5$$
Answer :
$${\log _{2}}5$$
35. If $$a, b, c, d$$ and $$p$$ are distinct real numbers such that $$\left( {{a^2} + {b^2} + {c^2}} \right){p^2} - 2\left( {ab + bc + cd} \right)p + \left( {{b^2} + {c^2} + {d^2}} \right) \leqslant 0$$ then $$a, b, c, d$$ are in
A
A.P.
B
G.P.
C
H.P.
D
None of these
Answer :
G.P.
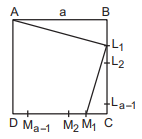
36. $$ABCD$$ is a square of length $$a,a \in N,a > 1.$$ Let $${L_1},{L_2},{L_3},.....$$ be points on $$BC$$ such that $$B{L_1} = {L_1}{L_2} = {L_2}{L_3} = ..... = 1$$ and $${M_1},{M_2},{M_3},.....$$ be point on $$CD$$ such that $$C{M_1} = {M_1}{M_2} = {M_2}{M_3} = ..... = 1.$$ Then $$\sum\limits_{n = 1}^{a - 1} {\left( {AL_n^2 + {L_n}M_n^2} \right)} $$ is equal to
A
$$\frac{1}{2}a{\left( {a - 1} \right)^2}$$
B
$$\frac{1}{2}a\left( {a - 1} \right)\left( {4a - 1} \right)$$
C
$$\frac{1}{2}\left( {a - 1} \right)\left( {2a - 1} \right)\left( {4a - 1} \right)$$
D
None of these
Answer :
$$\frac{1}{2}a\left( {a - 1} \right)\left( {4a - 1} \right)$$
37. Fifth term of a G.P. is 2, then the product of its 9 terms is
A
256
B
512
C
1024
D
none of these
Answer :
512
38. If $$a, b$$ and $$c$$ are in A.P., and $$p$$ and $$p'$$ are, respectively, A.M. and G.M. between $$a$$ and $$b$$ while $$q, q'$$ are, respectively, the A,M. and G. M. between $$b$$ and $$c$$ then
A
$${p^2} + {q^2} = p{'^2} + q{'^2}$$
B
$$pq = p'q'$$
C
$${p^2} - {q^2} = p{'^2} - q{'^2}$$
D
None of these
Answer :
$${p^2} - {q^2} = p{'^2} - q{'^2}$$
39. If $$x, y, z$$ are three real numbers of the same sign then the value of $$\frac{x}{y} + \frac{y}{z} + \frac{z}{x}$$ lies in the interval
A
$$\left[ {2, + \infty } \right)$$
B
$$\left[ {3, + \infty } \right)$$
C
$$\left( {3, + \infty } \right)$$
D
$$\left( { - \infty ,3} \right)$$
Answer :
$$\left[ {3, + \infty } \right)$$
40. If $$0 < x < \frac{\pi }{2}$$ then the minimum value of $${\left( {\sin x + \cos x + {\text{cosec}}\,2x} \right)^3}$$ is
A
27
B
13.5
C
6.75
D
none of these
Answer :
13.5