21. In a group of 50 people, two tests were conducted, one for diabetes and one for blood pressure. 30 people were diagnosed with diabetes and 40 people were diagnosed with high blood pressure. What is the minimum number of people who were having diabetes and high blood pressure ?
A
0
B
10
C
20
D
30
Answer :
20
22. If $$X$$ and $$Y$$ are two sets such that $$\left( {X \cup Y} \right)$$ has $$60$$ elements, $$X$$ has $$38$$ elements and $$Y$$ has $$42$$ elements, how many elements does $$\left( {X \cap Y} \right)$$ have ?
A
11
B
20
C
13
D
none of these
Answer :
20
23. Let $$R$$ = {(1,3), (4, 2), (2, 4), (2, 3), (3, 1)} be a relation on the set $$A$$ = {1, 2, 3, 4}. The relation $$R$$ is
A
reflexive
B
transitive
C
not symmetric
D
a function
Answer :
not symmetric
24. The number of linear function $$f$$ satisfying $$f\left( {x + f\left( x \right)} \right) = x + f\left( x \right)\,\forall \,x\, \in \,R$$ is :
A
0
B
1
C
2
D
3
Answer :
2
25. If $$f\left( x \right) = \frac{{\sin \left( {\left[ x \right]\pi } \right)}}{{{x^2} + x + 1}}$$ where $$\left[ . \right]$$ denotes the greatest integer function, then :
A
$$f$$ is one-one
B
$$f$$ is not one-one and non-constant
C
$$f$$ is a constant function
D
none of these
Answer :
$$f$$ is a constant function
26. Let $$f:\left[ {4,\,\infty } \right) \to \left[ {1,\,\infty } \right)$$ be a function defined by $$f\left( x \right) = {5^{x\left( {x - 4} \right)}},$$ then $${f^{ - 1}}\left( x \right)$$ is :
A
$$2 - \sqrt {4 + {{\log }_5}x} $$
B
$$2 + \sqrt {4 + {{\log }_5}x} $$
C
$${\left( {\frac{1}{5}} \right)^{x\left( {x - 4} \right)}}$$
D
None of these
Answer :
$$2 + \sqrt {4 + {{\log }_5}x} $$
27. If $$n\left( A \right) = 115,\,n\left( B \right) = 326,\,n\left( {A - B} \right) = 47,$$ then what is $$n\left( {A \cup B} \right)$$ equal to ?
A
373
B
165
C
370
D
394
Answer :
373
28.
What does the shaded portion of the Venn diagram below represent ?
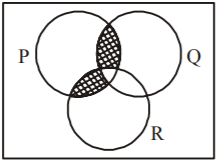
A
$$\left( {P \cap Q} \right) \cap \left( {P \cap R} \right)$$
B
$$\left( {\left( {P \cap Q} \right) - R} \right) \cup \left( {\left( {P \cap R} \right) - Q} \right)$$
C
$$\left( {\left( {P \cup Q} \right) - R} \right) \cap \left( {\left( {P \cap R} \right) - Q} \right)$$
D
$$\left( {\left( {P \cap Q} \right) \cup R} \right) \cap \left( {\left( {P \cup Q} \right) - R} \right)$$
Answer :
$$\left( {\left( {P \cap Q} \right) - R} \right) \cup \left( {\left( {P \cap R} \right) - Q} \right)$$
29. Let $$S$$ be any set and $$P\left( S \right)$$ be its power set. We define a relation $$R$$ on $$P\left( S \right)$$ by $$ARB$$ to mean $$A \subseteq B;\,\forall \,A,\,B\, \in \,P\left( S \right).$$ Then $$R$$ is :
A
equivalence relation
B
not an equivalence but partial order relation
C
both equivalence and partial order relation
D
none of these
Answer :
not an equivalence but partial order relation
30. $$R$$ is a relation over the set of real numbers and it is given by $$mn \geqslant 0.$$ Then $$R$$ is :
A
symmetric and transitive
B
reflexive and symmetric
C
a partial-order relation
D
an equivalence relation
Answer :
an equivalence relation