141. The curve $$\frac{{{x^n}}}{{{a^n}}} + \frac{{{y^n}}}{{{b^n}}} = 2$$ touches the line $$\frac{x}{a} + \frac{y}{b} = 2$$ at the point :
A
$$\left( {b,\,a} \right)$$
B
$$\left( {a,\,b} \right)$$
C
$$\left( {1,\,1} \right)$$
D
$$\left( {\frac{1}{b},\,\frac{1}{a}} \right)$$
Answer :
$$\left( {a,\,b} \right)$$
142. The normal to the curve $$x = a\left( {1 + \cos \theta } \right),y = a\,\sin \theta $$ at $$'\theta '$$ always passes through the fixed point
A
$$\left( {a,a} \right)$$
B
$$\left( {0,a} \right)$$
C
$$\left( {0,0} \right)$$
D
$$\left( {a,0} \right)$$
Answer :
$$\left( {a,0} \right)$$
143. Which one of the following curves cut the parabola $${y^2} = 4ax$$ at right angles?
A
$${x^2} + {y^2} = {a^2}$$
B
$$y = {e^{ - \frac{x}{{2a}}}}$$
C
$$y = ax$$
D
$${x^2} = 4ay$$
Answer :
$${x^2} = 4ay$$
144. If $$y = \int_0^x {\frac{{{t^2}}}{{\sqrt {{t^2} + 1} }}dt} $$ then the rate of change of $$y$$ with respect to $$x$$ when $$x=1,$$ is :
A
$$\sqrt 2 $$
B
$$\frac{1}{2}$$
C
$$\frac{1}{{\sqrt 2 }}$$
D
none of these
Answer :
$$\frac{1}{{\sqrt 2 }}$$
145. At what points of curve $$y = \frac{2}{3}{x^3} + \frac{1}{2}{x^2},$$ the tangent makes equal angle with the axis ?
A
$$\left( {\frac{1}{2},\,\frac{5}{{24}}} \right){\text{ and }}\left( { - 1,\, - \frac{1}{6}} \right)$$
B
$$\left( {\frac{1}{2},\,\frac{4}{9}} \right){\text{ and }}\left( { - 1,\,0} \right)$$
C
$$\left( {\frac{1}{3},\,\frac{1}{7}} \right){\text{ and }}\left( { - 3,\,\frac{1}{2}} \right)$$
D
$$\left( {\frac{1}{3},\,\frac{4}{{47}}} \right){\text{ and }}\left( { - 1,\, - \frac{1}{3}} \right)$$
Answer :
$$\left( {\frac{1}{2},\,\frac{5}{{24}}} \right){\text{ and }}\left( { - 1,\, - \frac{1}{6}} \right)$$
146. The fuel charges for running a train are proportional to the square of the speed generated in miles per hour and costs $$Rs.48$$ per hour at $$16$$ miles per hour. The most economical speed if the fixed charges i.e. salaries etc. amount to $$Rs.300$$ per hour is :
A
10
B
20
C
30
D
40
Answer :
40
147. If $$f\left( x \right) = \left( {ab - {b^2} - 2} \right)x + \int_0^x {\left( {{{\cos }^4}\,\theta + {{\sin }^4}\theta \,} \right)} d\theta $$ is a decreasing function of $$x$$ for all $$x\, \in \,R$$ and $$b\, \in \,R,\,b$$ being independent of $$x,$$ then :
A
$$a\, \in \,\left( {0,\,\sqrt 6 } \right)$$
B
$$a\, \in \,\left( { - \sqrt 6 ,\,\sqrt 6 } \right)$$
C
$$a\, \in \,\left( { - \sqrt 6 ,\,0} \right)$$
D
none of these
Answer :
$$a\, \in \,\left( { - \sqrt 6 ,\,\sqrt 6 } \right)$$
148. The function $$f\left( x \right) = {x^3} + \lambda {x^2} + 5x + \sin \,2x$$ will be an invertible function if $$\lambda $$ belongs to :
A
$$\left( { - \infty ,\, - 3} \right)$$
B
$$\left( { - 3,\,3} \right)$$
C
$$\left( {3,\, + \infty } \right)$$
D
none of these
Answer :
$$\left( { - 3,\,3} \right)$$
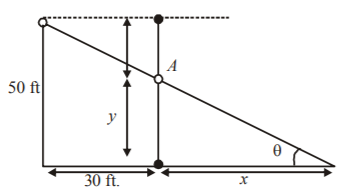
149. A lamp is $$50\,ft$$ above the ground. A ball is dropped from the same height from a point $$30\,ft$$ away from the light pole. If ball falls a distance $$s = 16{t^2}\,ft$$ in $$t$$ seconds, then the speed of the shadow of the ball moving along the ground $$\frac{1}{2}\,s$$ later is :
A
$$ - 1500\,ft/s$$
B
$$1500\,ft/s$$
C
$$ - 1600\,ft/s$$
D
$$1600\,ft/s$$
Answer :
$$ - 1500\,ft/s$$
150. Let $$f$$ and $$g$$ be functions from the interval $$\left[ {0,\,\infty } \right)$$ to the interval $$\left[ {0,\,\infty } \right),\,f$$ being an increasing and $$g$$ being a decreasing function. If $$f\left\{ {g\left( 0 \right)} \right\} = 0$$ then :
A
$$f\left\{ {g\left( x \right)} \right\} \geqslant f\left\{ {g\left( 0 \right)} \right\}$$
B
$$g\left\{ {f\left( x \right)} \right\} \leqslant g\left\{ {f\left( 0 \right)} \right\}$$
C
$$f\left\{ {g\left( 2 \right)} \right\} = 7$$
D
none of these
Answer :
$$g\left\{ {f\left( x \right)} \right\} \leqslant g\left\{ {f\left( 0 \right)} \right\}$$