121. If $$A,\,B$$ and $$C$$ are three finite sets, then what is $$\left[ {\left( {A \cup B} \right) \cap C} \right]'$$ equal to ?
A
$$A' \cup B' \cap C'$$
B
$$A' \cap B' \cap C'$$
C
$$A' \cap B' \cup C'$$
D
$$A \cap B \cap C$$
Answer :
$$A' \cap B' \cup C'$$
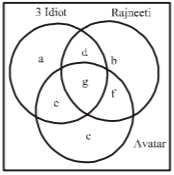
122. A survey shows that $$61\% ,\,46\% $$ and $$29\%$$ of the people watched "3 idiots", "Rajneeti" and "Avatar" respectively. $$25\%$$ people watched exactly two of the three movies and $$3\%$$ watched none. What percentage of people watched all the three movies ?
A
$$39\%$$
B
$$11\%$$
C
$$14\%$$
D
$$7\%$$
Answer :
$$7\%$$
123. Let $$f\left( x \right) = - 1 + \left| {x - 1} \right|,\, - 1 \leqslant x \leqslant 3$$ and $$ \leqslant g\left( x \right) = 2 - \left| {x + 1} \right|,\, - 2 \leqslant x \leqslant 2,$$ then $$\left( {fog} \right)\left( x \right)$$ is equal to :
A
\[\left\{ \begin{array}{l}
x + 1\,\,\,\,\, - 2 \le x \le 0\\
x - 1\,\,\,\,\,\,\,\,\,\,0 < x \le 2
\end{array} \right.\]
B
\[\left\{ \begin{array}{l}
x - 1\,\,\,\,\, - 2 \le x \le 0\\
x + 1\,\,\,\,\,\,\,\,\,\,\,0 < x \le 2
\end{array} \right.\]
C
\[\left\{ \begin{array}{l}
- 1 - x\,\,\,\,\, - 2 \le x \le 0\\
\,\,\,x - 1\,\,\,\,\,\,\,\,\,\,\,\,0 < x \le 2
\end{array} \right.\]
D
none of these
Answer :
none of these
124. In a class of $$30$$ pupils, $$12$$ take needle work, $$16$$ take physics and $$18$$ take history. If all the $$30$$ students take at least one subjects take and no one takes all three then the number of pupils taking $$2$$ subjects is :
A
16
B
6
C
8
D
20
Answer :
16
125. Let $$A$$ and $$B$$ be two sets. Then $$\left( {A \cup B} \right)' \cup \left( {A' \cap B} \right)$$ is equal to :
A
$$A'$$
B
$$A$$
C
$$B'$$
D
none of these
Answer :
$$A'$$
126. The inverse of $$f\left( x \right) = \frac{2}{3}\frac{{{{10}^x} - {{10}^{ - x}}}}{{{{10}^x} + {{10}^{ - x}}}}$$ is :
A
$$\frac{1}{3}\,{\log _{10}}\frac{{1 + x}}{{1 - x}}$$
B
$$\frac{1}{2}\,{\log _{10}}\frac{{2 + 3x}}{{2 - 3x}}$$
C
$$\frac{1}{3}\,{\log _{10}}\frac{{2 + 3x}}{{2 - 3x}}$$
D
$$\frac{1}{6}\,{\log _{10}}\frac{{2 - 3x}}{{2 + 3x}}$$
Answer :
$$\frac{1}{2}\,{\log _{10}}\frac{{2 + 3x}}{{2 - 3x}}$$
127. Let $$n\left( A \right) = 4$$ and $$n\left( B \right) = 6.$$ The number of one to one functions from A to B is :
A
$$24$$
B
$$60$$
C
$$120$$
D
$$360$$
Answer :
$$360$$
128. Let $$f\left( x \right) = \frac{x}{{1 + {x^2}}}$$ and $$g\left( x \right) = \frac{{{e^{ - x}}}}{{1 + \left[ x \right]}},$$ where $$\left[ x \right]$$ is the greatest integer less than or equal to $$x.$$ Then,
A
$$D\left( {f + g} \right) = R - \left[ { - 2,\,0} \right)$$
B
$$D\left( {f + g} \right) = R - \left[ { - 1,\,0} \right)$$
C
$$R\left( f \right) \cap R\left( g \right) = \left[ { - 2,\,\frac{1}{2}} \right]$$
D
None of these
Answer :
None of these
129. In a school, there are $$20$$ teachers who teach Mathematics or Physics of these, $$12$$ teach Mathematics and $$4$$ teach both Maths and Physics. Then the number of teachers teaching only Physics are :
A
$$4$$
B
$$8$$
C
$$12$$
D
$$16$$
Answer :
$$8$$
130. Let $$R$$ be a relation on $${\bf{N}} \times {\bf{N}}$$ defined by $$\left( {a,\,b} \right)R\left( {c,\,d} \right) \Rightarrow ad\left( {b + c} \right) = bc\left( {a + d} \right).\,R$$ is :
A
a particle order relation
B
an equivalence relation
C
an identity relation
D
none of these
Answer :
an equivalence relation