11. The domain of $${\sin ^{ - 1}}\left[ {{{\log }_3}\left( {\frac{x}{3}} \right)} \right]$$ is
A
[1, 9]
B
[-1, 9]
C
[- 9,1]
D
[-9,-1]
Answer :
[1, 9]
12. The graph of the function $$y = f\left( x \right)$$ is symmetrical about the line $$x = 2$$ then :
A
$$f\left( x \right) = - f\left( { - x} \right)$$
B
$$f\left( {2 + x} \right) = f\left( {2 - x} \right)$$
C
$$f\left( x \right) = f\left( { - x} \right)$$
D
$$f\left( {x + 2} \right) = f\left( {x - 2} \right)$$
Answer :
$$f\left( {2 + x} \right) = f\left( {2 - x} \right)$$
13. If $$f\left( x \right) = \cos \,\left[ \pi \right]x + \cos \,\left[ {\pi x} \right],$$ where $$\left[ y \right]$$ is the greatest integer function of $$y$$ then $$f\left( {\frac{\pi }{2}} \right)$$ is equal to :
A
$$\cos \,3$$
B
0
C
$$\cos \,4$$
D
none of these
Answer :
$$\cos \,4$$
14. Let $$f\left( x \right) = \left[ x \right] = $$ the greatest integer less than or equal to $$x$$ and $$g\left( x \right) = x - \left[ x \right].$$ Then for any two real numbers $$x$$ and $$y$$
A
$$f\left( {x + y} \right) = f\left( x \right) + f\left( y \right)$$
B
$$g\left( {x + y} \right) = g\left( x \right) + g\left( y \right)$$
C
$$f\left( {x + y} \right) = f\left( x \right) + f\left\{ {y + g\left( x \right)} \right\}$$
D
none of these
Answer :
$$f\left( {x + y} \right) = f\left( x \right) + f\left\{ {y + g\left( x \right)} \right\}$$
15.
The domain of the function
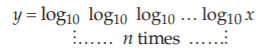
is :
A
$$\left[ {{{10}^n},\, + \infty } \right)$$
B
$$\left( {{{10}^{n - 1}},\, + \infty } \right)$$
C
$$\left( {{{10}^{n - 2}},\, + \infty } \right)$$
D
none of these
Answer :
none of these
16. If $$f\left( x \right) = {x^2} + 2bx + 2{c^2}$$ and $$g\left( x \right) = - {x^2} - 2cx + {b^2}$$ such that min $$\min \,f\left( x \right) > \max \,g\left( x \right),$$ then the relation between $$b$$ and $$c,$$ is
A
no real value of $$b$$ & $$c$$
B
$$0 < c < b\sqrt 2 $$
C
$$\left| c \right| < \left| b \right|\sqrt 2 $$
D
$$\left| c \right| > \left| b \right|\sqrt 2 $$
Answer :
$$\left| c \right| > \left| b \right|\sqrt 2 $$
17. A real valued function $$f\left( x \right)$$ satisfies the functional equation $$f\left( {x - y} \right) = f\left( x \right)f\left( y \right) - f\left( {a - x} \right)f\left( {a + y} \right)$$ where $$a$$ is a given constant and $$f\left( 0 \right) = 1,\,f\left( {2a - x} \right)$$ is equal to :
A
$$ - f\left( x \right)$$
B
$$f\left( x \right)$$
C
$$f\left( a \right) + f\left( {a - x} \right)$$
D
$$f\left( { - x} \right)$$
Answer :
$$ - f\left( x \right)$$
18. The domain of the function $$f\left( x \right) = \sqrt {{x^2} - {{\left[ x \right]}^2}} ,$$ where $$\left[ x \right] = $$ the greatest integer less than or equal to $$x,$$ is :
A
$$R$$
B
$$\left[ {0,\, + \infty } \right)$$
C
$$\left( { - \infty ,\,0} \right]$$
D
none of these
Answer :
none of these
19. The domain of the function $$f\left( x \right) = \frac{{\left| {x + 3} \right|}}{{x + 3}}$$ is :
A
$$\left\{ { - 3} \right\}$$
B
$$R - \left\{ { - 3} \right\}$$
C
$$R - \left\{ 3 \right\}$$
D
$$R$$
Answer :
$$R - \left\{ { - 3} \right\}$$
20. The domain of the function $$\sqrt {{x^2} - 5x + 6} + \sqrt {2x + 8 - {x^2}} $$ is :
A
$$\left[ {2,\,3} \right]$$
B
$$\left[ { - 2,\,4} \right]$$
C
$$\left[ { - 2,\,2} \right] \cup \left[ {3,\,4} \right]$$
D
$$\left[ { - 2,\,1} \right] \cup \left[ {2,\,4} \right]$$
Answer :
$$\left[ { - 2,\,2} \right] \cup \left[ {3,\,4} \right]$$

PNG.PNG)