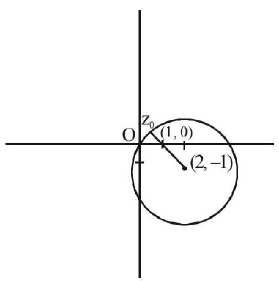61. Let $$\alpha \,{\text{and }}\beta $$ be two roots of the equation $${x^2} + 2x + 2 = 0,$$ then $${\alpha ^{15}} + {\beta ^{15}}$$ is equal to:
A
$$- 256$$
B
$$512$$
C
$$- 512$$
D
$$256$$
Answer :
$$- 256$$
62. If $$\left| z \right| = 1$$ then $$\frac{{1 + z}}{{1 + \overline z }}$$ is equal to
A
$$z$$
B
$${ \overline z }$$
C
$${z + \overline z }$$
D
None of these
Answer :
$$z$$
63. If $$\alpha $$ is non-real and $$\alpha = \root 5 \of 1 $$ then the value of $${2^{\left| {1 + \alpha + {\alpha ^2} + {\alpha ^{ - 2}} - {\alpha ^{ - 1}}} \right|}}$$ is equal to
A
4
B
2
C
1
D
None of these
Answer :
2
64. Let $$S$$ be the set of all complex numbers $$z$$ satisfying $$\left| {z - 2 + i} \right|\, \geqslant \sqrt 5 .$$ If the complex number $${z_0}$$ is such that $$\frac{1}{{\left| {{z_0} - 1} \right|}}$$ is the maximum of the set $$\left\{ {\frac{1}{{\left| {z - 1} \right|}}:z \in S} \right\},$$ then the principal argument of $$\frac{{4 - {z_0} - {{\overline z }_0}}}{{{z_0} - {{\overline z }_0} + 2i}}$$ is
A
$$\frac{\pi }{4}$$
B
$$\frac{{3\pi }}{4}$$
C
$$\frac{\pi }{2}$$
D
$$ - \frac{\pi }{2}$$
Answer :
$$ - \frac{\pi }{2}$$
65. The value of the sum $$\sum\limits_{n = 1}^{13} {\left( {{i^n} + {i^{n + 1}}} \right)} ;$$ where $$i = \sqrt { - 1} $$ is :
A
$$i$$
B
$$- i$$
C
$$0$$
D
$$i - 1$$
Answer :
$$i - 1$$
66. If $$z$$ is a complex number such that $$z + \left| z \right| = 8 + 12i,$$ then the value of $$\left| {{z^2}} \right|$$ is equal to
A
228
B
144
C
121
D
169
Answer :
169
67. The greatest and the least value of $$\left| {{z_1} + {z_2}} \right|$$ if $$z_1 = 24 + 7i$$ and $$\left| {{z_2}} \right| = 6$$ respectively are
A
$$25, 19$$
B
$$19, 25$$
C
$$ - 19, - 25$$
D
$$- 25, - 19$$
Answer :
$$25, 19$$
68. The value of $${\left( {1 + 2\omega + {\omega ^2}} \right)^{3n}} - {\left( {1 + \omega + 2{\omega ^2}} \right)^{3n}}$$ is :
A
$$0$$
B
$$1$$
C
$${{\omega }}$$
D
$${{\omega ^2}}$$
Answer :
$$0$$
69. $$\left| {\frac{{z - 1}}{{z + 1}}} \right| = 1$$ represents
A
a circle
B
an ellipse
C
a straight line
D
None of these
Answer :
a straight line
70. If $${x^3} - 1 = 0$$ has the non-real complex roots $$\alpha ,\beta $$ then the value of $${\left( {1 + 2\alpha + \beta } \right)^3} - {\left( {3 + 3\alpha + 5\beta } \right)^3}$$ is
A
$$- 7$$
B
$$6$$
C
$$- 5$$
D
$$0$$
Answer :
$$- 7$$