41.
If $$1,\omega ,{\omega ^2}$$ are the three cube roots of unity, then what is $$\frac{{\left( {a{\omega ^6} + b{\omega ^4} + c{\omega ^2}} \right)}}{{\left( {b + c{\omega ^{10}} + a{\omega ^8}} \right)}}$$ equal to ? A
$$\frac{a}{b}$$
B
$$b$$
C
$$\omega $$
D
$$\omega^2 $$
Answer :
$$\omega $$
View Solution
Discuss Question
$$1,\omega $$ and $$\omega^2 $$ are the three cube roots of unity.
42.
If $$\left| {{z_1}} \right| = \left| {{z_2}} \right| = .....\left| {{z_n}} \right| = 1,$$ then the value of $$\left| {{z_1} + {z_2} + ..... {z_n}} \right| - \left| {\frac{1}{{{z_1}}} + \frac{1}{{{z_2}}} + ..... + \frac{1}{{{z_n}}}} \right|$$ is, A
$$0$$
B
$$1$$
C
$$- 1$$
D
None
Answer :
$$0$$
View Solution
Discuss Question
$$\eqalign{
& {z_1}{{\bar z}_1} = {z_2}{{\bar z}_2} = ..... = {z_n}{{\bar z}_n} = 1 \cr
& \Rightarrow \,{{\bar z}_1} = \frac{1}{{{z_1}}},{{\bar z}_2} = \frac{1}{{{z_2}}},{{\bar z}_3} = \frac{1}{{{z_3}}},.....,{{\bar z}_n} = \frac{1}{{{z_n}}} \cr
& \therefore \,\left| {{z_1} + {z_2} + ..... + {z_n}} \right| - \left| {\frac{1}{{{z_1}}} + \frac{1}{{{z_2}}} + ..... + \frac{1}{{{z_n}}}} \right| \cr
& = \,\left| {{z_1} + {z_2} + ..... + {z_n}} \right| - \left| {{{\bar z}_1} + {{\bar z}_2} + ..... + {{\bar z}_n}} \right| = 0 \cr} $$
43.
If $$\left| {{z_1} - 1} \right| < 1,\left| {{z_2} - 2} \right| < 2,\left| {{z_3} - 3} \right| < 3$$ then $$\left| {{z_1} + {z_2} + {z_3}} \right|$$ A
is less than 6
B
is more than 3
C
is less than 12
D
lies between 6 and 12
Answer :
is less than 12
View Solution
Discuss Question
$$\left| {{z_1} + {z_2} + {z_3}} \right| = \left| {\left( {{z_1} - 1} \right) + \left( {{z_2} - 2} \right) + \left( {{z_3} - 3} \right) + 6} \right| \leqslant \left| {{z_1} - 1} \right| + \left| {{z_2} - 2} \right| + \left| {{z_3} - 3} \right| + 6 < 1 + 2 + 3 + 6.$$
44.
If $$\left| {{z_1}} \right| = \left| {{z_2}} \right| = \left| {{z_3}} \right| = \left| {{z_4}} \right|$$ then the points representing $${z_1},{z_2},{z_3},{z_4}$$ are A
concyclic
B
vertices of a square
C
vertices of a rhombus
D
None of these
Answer :
concyclic
View Solution
Discuss Question
$$\left| {{z_1}} \right| = $$ the distance of the point representing $${{z_1}}$$ from the origin. So, the distances of the four points from the origin are equal
45.
If $$\left( {a + ib} \right)\left( {c + id} \right)\left( {e + if} \right)\left( {g + ih} \right) = A + iB,$$ then $$\left( {{a^2} + {b^2}} \right)\left( {{c^2} + {d^2}} \right)\left( {{e^2} + {f^2}} \right)\left( {{g^2} + {h^2}} \right) = $$ A
$${A^2} + {B^2}$$
B
$${A^2} - {B^2}$$
C
$$A^2$$
D
$$B^2$$
Answer :
$${A^2} + {B^2}$$
View Solution
Discuss Question
$$\eqalign{
& \left( {a + ib} \right)\left( {c + id} \right)\left( {e + if} \right)\left( {g + ih} \right) = A + iB\,\,\,\,.....\left( {\text{i}} \right) \cr
& \Rightarrow \,\left( {a - ib} \right)\left( {c - id} \right)\left( {e - if} \right)\left( {g - ih} \right) = A - iB\,\,\,.....\left( {{\text{ii}}} \right) \cr} $$
46.
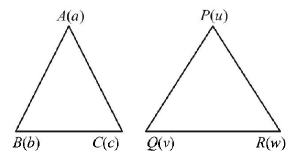
If $$a, b, c$$ and $$u, v, w$$ are complex numbers representing the vertices of two triangles such that $$c = \left( {1 - r} \right)a + rb\,\,{\text{and }}w = \left( {1 - r} \right)u + rv,$$ where $$r$$ is a complex number, then the two triangles A
have the same area
B
are similar
C
are congruent
D
none of these
Answer :
are similar
View Solution
Discuss Question
Let $$ABC$$ be the $$\Delta $$ with vertices $$a, b, c$$ and $$PQR$$ be the $$\Delta $$ with vertices $$u, v, w.$$
Then $$c = (1 - r)a + rb$$
$$\eqalign{
& \Rightarrow \,\,c - a = r\left( {b - a} \right) \cr
& \Rightarrow \,\,\frac{{c - a}}{{b - a}} = r\,\,\,\,\,......\left( 1 \right) \cr
& \Rightarrow \,\,w = \left( {1 - r} \right)u + rv \cr
& \Rightarrow \,\,\frac{{w - u}}{{v - u}} = r\,\,\,\,......\left( 2 \right) \cr} $$
From (1) and (2) $$\left| {\frac{{c - a}}{{b - a}}} \right| = \left| {\frac{{w - u}}{{v - u}}} \right|\,\,{\text{and}}$$
$$\eqalign{
& {\text{arg}}\left( {\frac{{c - a}}{{b - a}}} \right) = {\text{arg}}\left( {\frac{{w - u}}{{v - u}}} \right) \cr
& \Rightarrow \,\,\frac{{AC}}{{AB}} = \frac{{PR}}{{PQ}}\,\,{\text{and }}\angle CAB = \angle RPQ \cr
& \Rightarrow \,\,\Delta ABC \sim \Delta PQR \cr} $$
47.
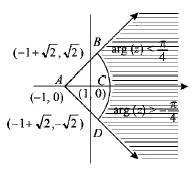
The locus of $$z$$ which lies in shaded region (excluding the boundaries) is best represented by
A
$$z:\left| {z + 1} \right| > 2\,\,{\text{and }}\left| {\arg \left( {z + 1} \right)} \right| < \frac{\pi }{4}$$
B
$$z:\left| {z - 1} \right| > 2\,\,{\text{and }}\left| {\arg \left( {z - 1} \right)} \right| < \frac{\pi }{4}$$
C
$$z:\left| {z + 1} \right| < 2\,\,{\text{and }}\left| {\arg \left( {z + 1} \right)} \right| < \frac{\pi }{2}$$
D
$$z:\left| {z - 1} \right| < 2\,\,{\text{and }}\left| {\arg \left( {z + 1} \right)} \right| < \frac{\pi }{2}$$
Answer :
$$z:\left| {z + 1} \right| > 2\,\,{\text{and }}\left| {\arg \left( {z + 1} \right)} \right| < \frac{\pi }{4}$$
View Solution
Discuss Question
Here we observe that.
48.
The points $${z_1},{z_2},{z_3},{z_4}$$ in the complex plane are the vertices of a parallelogram taken in order if and only if A
$${z_1} + {z_4} = {z_2} + {z_3}$$
B
$${z_1} + {z_3} = {z_2} + {z_4}$$
C
$${z_1} + {z_2} = {z_3} + {z_4}$$
D
None of these
Answer :
$${z_1} + {z_3} = {z_2} + {z_4}$$
View Solution
Discuss Question
If vertices of a parallelogram are $${z_1},{z_2},{z_3},{z_4}$$ then as diagonals bisect each other
49.
If $${x^2} - x + 1 = 0$$ then the value of $${\sum\limits_{n = 1}^5 {\left( {{x^n} + \frac{1}{{{x^n}}}} \right)} ^2}$$ is A
8
B
10
C
12
D
None of these
Answer :
8
View Solution
Discuss Question
$$\eqalign{
& x = \frac{{1 \pm \sqrt {3i} }}{2} = \cos \frac{\pi }{3} \pm i\sin \frac{\pi }{3} \cr
& \therefore \,\,{x^{2n}} = \cos \frac{{2n\pi }}{3} \pm i\sin \frac{{2n\pi }}{3} \cr
& {\text{or,}}\,\,{\left( {{x^n} + \frac{1}{{{x^n}}}} \right)^2} = {x^{2n}} + {x^{ - 2n}} + 2 \cr
& {\text{or,}}\,\,{\left( {{x^n} + \frac{1}{{{x^n}}}} \right)^2} = \cos \frac{{2n\pi }}{3} \pm i\sin \frac{{2n\pi }}{3} + \cos \frac{{2n\pi }}{3} \mp i\sin \frac{{2n\pi }}{3} + 2 \cr
& {\text{or,}}\,\,{\left( {{x^n} + \frac{1}{{{x^n}}}} \right)^2} = 2 + 2\cos \frac{{2n\pi }}{3}. \cr} $$
50.
If the roots of $${z^3} + i{z^2} + 2i = 0$$ represent the vertices of a $$\vartriangle ABC$$ in the Argand plane then the area of the triangle is A
$$\frac{{3\sqrt 7 }}{2}$$
B
$$\frac{{3\sqrt 7 }}{4}$$
C
$$2$$
D
None of these
Answer :
$$2$$
View Solution
Discuss Question
$$\eqalign{
& \left( {z - i} \right)\left( {{z^2} + 2iz - 2} \right) = 0 \cr
& \Rightarrow \,\,z = i,\frac{{ - 2i \pm \sqrt {4{i^2} + 8} }}{2} = i,1 - i, - 1 - i. \cr} $$