201.
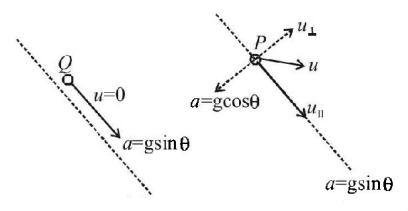
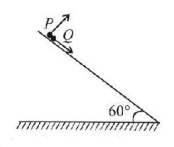
A particle $$P$$ is projected from a point on the surface of smooth inclined plane (see figure). Simultaneously another particle $$Q$$ is released on the from smooth the same inclined position. plane $$P$$ and $$Q$$ collide on the in clined plane after $$t = 4$$ second. The speed of projection of $$P$$ is
A
$$5\,m/s$$
B
$$10\,m/s$$
C
$$15\,m/s$$
D
$$20\,m/s$$
Answer :
$$10\,m/s$$
202. If the magnitude of sum of two vectors is equal to the magnitude of difference of the two vectors, the angle between these vectors is
A
$${90^ \circ }$$
B
$${45^ \circ }$$
C
$${180^ \circ }$$
D
$${0^ \circ }$$
Answer :
$${90^ \circ }$$
203.
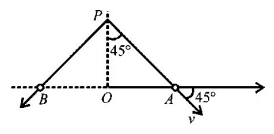
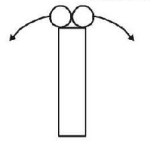
Two identical particles are projected horizontally in opposite directions with a speed of $$5\,m{s^{ - 1}}$$ each from the top of a tall tower as shown. Assuming $$g = 10\,m{s^{ - 2}},$$ the distance between them at the moment when their velocity vectors become mutually perpendicular is
A
$$2.5\,m$$
B
$$5\,m$$
C
$$10\,m$$
D
$$20\,m$$
Answer :
$$5\,m$$
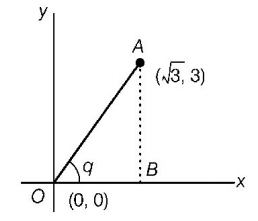
204. A particle starting from the origin $$\left( {0,0} \right)$$ moves in a straight line in the $$\left( {x,y} \right)$$ plane. Its co-ordinates at a later time are $$\left( {\sqrt 3 ,3} \right).$$ The path of the particle makes with the $$x$$-axis an angle of
A
$${30^ \circ }$$
B
$${45^ \circ }$$
C
$${60^ \circ }$$
D
$${0^ \circ }$$
Answer :
$${60^ \circ }$$
205. If $$\vec A = 5\hat i + 7\hat j - 3\hat k$$ and $$\vec B = 2\hat i + 2\hat j - a\hat k$$ are perpendicular vectors, the value of $$a$$ is:
A
$$- 2$$
B
$$8$$
C
$$-7$$
D
$$- 8$$
Answer :
$$- 8$$
206. A man throws balls with same speed vertically upwards one after the other at an interval of $$2\,\sec .$$ What should be the speed of throw so that more than two balls are in air at anytime?
A
Only with speed $$19.6\,m/s$$
B
More than $$19.6\,m/s$$
C
At least $$9.8\,m/s$$
D
Any speed less then $$19.6\,m/s.$$
Answer :
More than $$19.6\,m/s$$
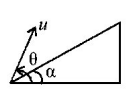
207. A particle of mass $$m$$ is projected with velocity $$v$$ making an angle of $${45^ \circ }$$ with the horizontal. When the particle lands on the level ground, the magnitude of the change in its momentum will be
A
$$2mv$$
B
$$\frac{{mv}}{{\sqrt 2 }}$$
C
$$mv\sqrt 2 $$
D
zero
Answer :
$$mv\sqrt 2 $$
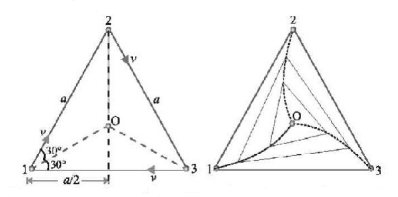
208. Three points are located at the vertices of an equilateral triangle whose side equal to $$a.$$ They all start moving simultaneously with velocity $$v$$ constant in modulus, with first point heading continually for the second, the second for the third, and the third for the first. How soon will the points converge?
A
$$\frac{{3v}}{{2a}}$$
B
$$\frac{{2a}}{{5v}}$$
C
$$\frac{{5v}}{{3a}}$$
D
$$\frac{{2a}}{{3v}}$$
Answer :
$$\frac{{2a}}{{3v}}$$
209.
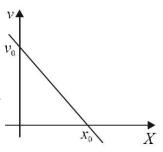
The velocity-displacement graph of a particle moving along a straight line is shown
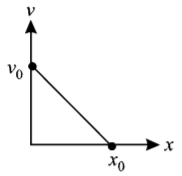
The most suitable acceleration-displacement graph will be-
A
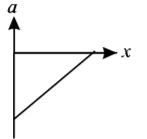

B
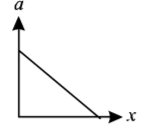

C
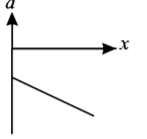

D

Answer :


210. For a stone thrown from a lower of unknown height, the maximum range for a projection speed of $$10\,m/s$$ is obtained for a projection angle of $${30^ \circ }.$$ The corresponding distance between the foot of the lower and the point of landing of the stone is
A
$$10\,m$$
B
$$20\,m$$
C
$$\left( {\frac{{20}}{{\sqrt 3 }}} \right)m$$
D
$$\left( {\frac{{10}}{{\sqrt 3 }}} \right)m$$
Answer :
$$\left( {\frac{{10}}{{\sqrt 3 }}} \right)m$$