271.
In $$1.0\,s,$$ a particle goes from point $$A$$ to point $$B,$$ moving in a semicircle of radius $$1.0 \,m$$ (see Figure). The magnitude of the average velocity-

A
$$3.14 \,m/s$$
B
$$2.0 \,m/s$$
C
$$1.0 \,m/s$$
D
Zero
Answer :
$$2.0 \,m/s$$
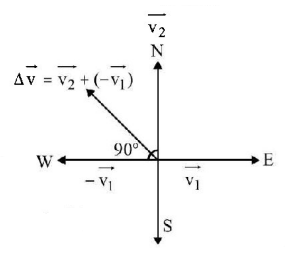
272. A particle is moving eastwards with a velocity of $$5\,m{s^{ - 1}}.$$ In 10 seconds the velocity changes to $$5\,m{s^{ - 1}}$$ northwards. The average acceleration in this time is
A
$$\frac{1}{2}m{s^{ - 2}}$$ towards north
B
$$\frac{1}{{\sqrt 2 }}m{s^{ - 2}}$$ towards north - east
C
$$\frac{1}{{\sqrt 2 }}m{s^{ - 2}}$$ towards north - west
D
zero
Answer :
$$\frac{1}{{\sqrt 2 }}m{s^{ - 2}}$$ towards north - west
273. The distance travelled by a particle starting from rest and moving with an acceleration $$\frac{4}{3}m{s^{ - 2}},$$ in the third second is:
A
$$6\,m$$
B
$$4\,m$$
C
$$\frac{{10}}{3}m$$
D
$$\frac{{19}}{3}m$$
Answer :
$$\frac{{10}}{3}m$$
274. Two trains, each $$40\,m$$ long are travelling in opposite direction with equal velocity $$20\,m/s.$$ The time of crossing is
A
$$1s$$
B
$$2s$$
C
$$3s$$
D
Zero
Answer :
$$2s$$
275. The ball is projected up from ground with speed $$30\,m/\sec .$$ What is the average velocity for time 0 to $$4\,\sec $$ ?
A
$$10\,m/\sec $$
B
$$20\,m/\sec $$
C
$$15\,m/\sec $$
D
zero
Answer :
$$10\,m/\sec $$
276. The position $$x$$ of a particle w.r.t. time $$t$$ along $$x$$-axis is given by $$x = 9{t^2} - {t^3},$$ where $$x$$ is in metre and $$t$$ in $$sec.$$ What will be the position of this particle when it achieves maximum speed along the $$+ x$$ direction?
A
$$32\,m$$
B
$$54\,m$$
C
$$81\,m$$
D
$$24\,m$$
Answer :
$$54\,m$$
277. A stone is dropped into a well in which the level of water is $$h$$ below the top of the well. If $$v$$ is velocity of sound, the time $$T$$ after which the splash is heard is given by
A
$$T = \frac{{2h}}{v}$$
B
$$T = \sqrt {\left( {\frac{{2h}}{g}} \right)} + \frac{h}{v}$$
C
$$T = \sqrt {\left( {\frac{{2h}}{v}} \right)} + \frac{h}{g}$$
D
$$T = \sqrt {\left( {\frac{h}{{2g}}} \right)} + \frac{{2h}}{v}$$
Answer :
$$T = \sqrt {\left( {\frac{{2h}}{g}} \right)} + \frac{h}{v}$$
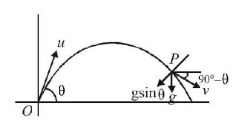
278. If a particle is projected with speed $$u$$ from ground at an angle with horizontal ,then radius of curvature of a point where velocity vector is perpendicular to initial velocity vector is given by
A
$$\frac{{{u^2}{{\cos }^2}\theta }}{g}$$
B
$$\frac{{{u^2}{{\cot }^2}\theta }}{{g\sin \theta }}$$
C
$$\frac{{{u^2}}}{g}$$
D
$$\frac{{{u^2}{{\tan }^2}\theta }}{{g\cos \theta }}$$
Answer :
$$\frac{{{u^2}{{\cot }^2}\theta }}{{g\sin \theta }}$$
279. If $${V_r}$$ is the velocity of rain falling vertically and $${V_m}$$ is the velocity of a man walking on a level road, and $$\theta $$ is the angle with vertical at which he should hold the umbrella to protect himself, than the relative velocity of rain w.r.t. the man is given by:
A
$${V_{rm}} = \sqrt {V_r^2 + V_m^2 + 2{V_r}{V_m}\cos \theta } $$
B
$${V_{rm}} = \sqrt {V_r^2 + V_m^2 - 2{V_r}{V_m}\cos \theta } $$
C
$${V_{rm}} = \sqrt {V_r^2 + V_m^2} $$
D
$${V_{rm}} = \sqrt {V_r^2 - V_m^2} $$
Answer :
$${V_{rm}} = \sqrt {V_r^2 + V_m^2} $$
280.
The graph shown below represent

A
$$A$$ and $$B$$ are moving with same velocity in opposite directions
B
velocity of $$B$$ is more than $$A$$ in same direction
C
velocity of $$A$$ is more than $$B$$ in same direction
D
velocity of $$A$$ and $$B$$ is equal in same direction
Answer :
velocity of $$A$$ and $$B$$ is equal in same direction