251.
A cricket ball is hit with a velocity $$25\,m{s^{ - 1}},{60^ \circ }$$ above the horizontal. How far above the ground, ball passes over a fielder $$50\,m$$ from the bat (consider the ball is struck very close to the ground)?
Take $$\sqrt 3 = 1.7$$ and $$g = 10\,m{s^{ - 2}}$$
A
$$6.8\,m$$
B
$$7\,m$$
C
$$5\,m$$
D
$$10\,m$$
Answer :
$$5\,m$$
252. A body is thrown with a velocity of $$9.8\,m{s^{ - 1}}$$ making an angle of $${30^ \circ }$$ with the horizontal. It will hit the ground after a time
A
$$3.0\,s$$
B
$$2.0\,s$$
C
$$1.5\,s$$
D
$$1\,s$$
Answer :
$$1\,s$$
253. A body is thrown vertically upwards. If air resistance is to be taken into account, then the time during which the body rises is [assume no air resistance close to earth]
A
equal to the time of fall
B
less than the time of fall
C
greater than the time of fall
D
twice the time of fall
Answer :
less than the time of fall
254. The position of particle is given by $$\vec r = 2{t^2}\hat i + 3t\hat j + 4\hat k,$$ where $$t$$ is in second and the coefficients have proper units for $${\vec r}$$ to be in metre. The $$\vec a\left( t \right)$$ of the particle at $$t = 1\,s$$ is
A
$$4\,m{s^{ - 2}}$$ along $$y$$-direction
B
$$3\,m{s^{ - 2}}$$ along $$x$$-direction
C
$$4\,m{s^{ - 2}}$$ along $$x$$-direction
D
$$2\,m{s^{ - 2}}$$ along $$z$$-direction
Answer :
$$4\,m{s^{ - 2}}$$ along $$x$$-direction
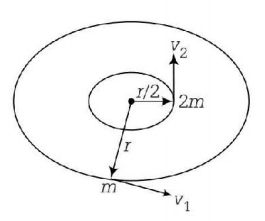
255. Two stones of masses $$m$$ and $$2\,m$$ are whirled in horizontal circles, the heavier one in a radius $$\frac{r}{2}$$ and the lighter one in radius $$r.$$ The tangential speed of lighter stone is $$n$$ times that of the value of heavier stone when they experience same centripetal forces. The value of $$n$$ is
A
2
B
3
C
4
D
1
Answer :
2
256.
A body is projected from the ground with a velocity $$50\,m/s$$ at an angle of $${30^ \circ }.$$ It crosses a wall after $$3\,\sec .$$ How far beyond the wall the stone will strike the ground?
[take $$g = 10\,m/{s^2}$$ ]
A
$$50\sqrt 3 $$
B
$$70\sqrt 2 $$
C
$$15\sqrt 3 $$
D
$$16\sqrt 2 $$
Answer :
$$50\sqrt 3 $$
257. A train of $$150\,m$$ length is going towards north direction at a speed of $$10\,m{s^{ - 1}}.$$ A parrot flies at a speed of $$5\,m{s^{ - 1}}$$ towards south direction parallel to the railway track. The time taken by the parrot to cross the train is equal to
A
$$12\,s$$
B
$$8\,s$$
C
$$15\,s$$
D
$$10\,s$$
Answer :
$$10\,s$$
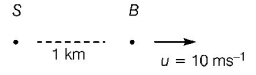
258. A bus is moving with a speed of $$10\,m{s^{ - 1}}$$ on a straight road. A scooterist wishes to overtake the bus in $$100\,s.$$ If the bus is at a distance of $$1\,km$$ from the scooterist, with what speed should the scooterist chase the bus?
A
$$20\,m{s^{ - 1}}$$
B
$$40\,m{s^{ - 1}}$$
C
$$25\,m{s^{ - 1}}$$
D
$$10\,m{s^{ - 1}}$$
Answer :
$$20\,m{s^{ - 1}}$$
259. A car moving with a speed of $$40\,km/h$$ can be stopped after $$2\,m$$ by applying brakes. If the same car is moving with a speed of $$80\,km/h,$$ what is the minimum stopping distance?
A
$$8\,m$$
B
$$2\,m$$
C
$$4\,m$$
D
$$6\,m$$
Answer :
$$8\,m$$
260. A particle is projected at angle $${37^ \circ }$$ with the incline plane in upward direction with speed $$10\,m/s.$$ The angle of incline plane is given $${53^ \circ }.$$ Then the maximum height attained by the particle from the incline plane will be
A
$$3\,m$$
B
$$4\,m$$
C
$$5\,m$$
D
zero
Answer :
$$3\,m$$