241. A projectile is fired from the surface of the earth with a velocity of $$5\,m{s^{ - 1}}$$ at angle $$\theta $$ with the horizontal. Another projectile fired from another planet with a velocity of $$3\,m{s^{ - 1}}$$ at the same angle follows a trajectory which is identical with the trajectory of the projectile fired from the earth. The value of the acceleration due to gravity on the planet is (in $$m{s^{ - 2}}$$ ) is (given, $$g = 9.8\,m{s^{ - 2}}$$ )
A
$$3.5$$
B
$$5.9$$
C
$$16.3$$
D
$$110.8$$
Answer :
$$3.5$$
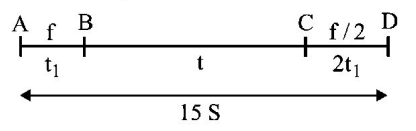
242. A car, starting from rest, accelerates at the rate $$f$$ through a distance $$S,$$ then continues at constant speed for time $$t$$ and then decelerates at the rate $$\frac{f}{2}$$ to come to rest. If the total distance traversed is $$15\,S,$$ then
A
$$S = \frac{1}{6}f{t^2}$$
B
$$S = ft$$
C
$$S = \frac{1}{4}f{t^2}$$
D
$$S = \frac{1}{{72}}f{t^2}$$
Answer :
$$S = \frac{1}{{72}}f{t^2}$$
243. A body is projected vertically upwards. If $${t_1}$$ and $${t_2}$$ be the times at which it is at height $$h$$ above the projection while ascending and descending respectively, then $$h$$ is
A
$$\frac{1}{2}g{t_1}{t_2}$$
B
$$g{t_1}{t_2}$$
C
$$2g{t_1}{t_2}$$
D
$$2hg$$
Answer :
$$\frac{1}{2}g{t_1}{t_2}$$
244. The displacement $$x$$ of a particle along a straight line at time $$t$$ is given by : $$x = {a_0} + \frac{{{a_1}t}}{2} + \frac{{{a_2}}}{3}{t^2}.$$ The acceleration of the particle is
A
$$\frac{{{a_2}}}{3}$$
B
$$\frac{{2{a_2}}}{3}$$
C
$$\frac{{{a_1}}}{2}$$
D
$${a_0} + \frac{{{a_2}}}{3}$$
Answer :
$$\frac{{2{a_2}}}{3}$$
245. A large number of bullets are fired in all directions with the same speed $$v.$$ What is the maximum area on the ground on which these bullets will spread?
A
$$\frac{{\pi {v^2}}}{g}$$
B
$$\frac{{\pi {v^4}}}{{{g^2}}}$$
C
$${\pi ^2}\frac{{{v^2}}}{{{g^2}}}$$
D
$$\frac{{{\pi ^2}{v^4}}}{{{g^2}}}$$
Answer :
$$\frac{{\pi {v^4}}}{{{g^2}}}$$
246. A bird flies with a speed of $$10\,km/h$$ and a car moves with uniform speed of $$8\,km/h.$$ Both start from $$B$$ towards $$A\left( {BA = 40\,km} \right)$$ at the same instant. The bird having reached $$A,$$ flies back immediately to meet the approaching car. As soon as it reaches the car, it flies back to $$A.$$ The bird repeats this till both the car and the bird reach $$A$$ simultaneously. The total distance flown by the bird is
A
$$80\,km$$
B
$$40\,km$$
C
$$50\,km$$
D
$$30\,km$$
Answer :
$$50\,km$$
247. The velocity of an object moving rectilinearly is given as a function of time by $$v = 4{t^2} - 3{t^2},$$ where $$v$$ is in $$m/s$$ and $$t$$ is in seconds. The average velocity of particle between $$t = 0$$ to $$t = 2$$ seconds is
A
$$0$$
B
$$- 2m/s$$
C
$$- 4m/s$$
D
$$8m/s$$
Answer :
$$0$$
248. A body starts from rest and is uniformly accelerated for $$30\,s.$$ The distance travelled in the first $$10s$$ is $${x_1},$$ next $$10\,s$$ is $${x_2}$$ and the last $$10\,s$$ is $${x_3}.$$ Then $${x_1}:{x_2}:{x_3}$$ is the same as:
A
$$1:2:4$$
B
$$1:2:5$$
C
$$1:3:5$$
D
$$1:3:9$$
Answer :
$$1:3:5$$
249. A projectile is given an initial velocity of $$\left( {\hat i + 2\hat j} \right)m/s$$ where $${\hat i}$$ is along the ground and $${\hat j}$$ is along the vertical. If $$g = 10\,m/{s^2},$$ the equation of its trajectory is :
A
$$y = x - 5{x^2}$$
B
$$y = 2x - 5{x^2}$$
C
$$4y = 2x - 5{x^2}$$
D
$$4y = 2x - 25{x^2}$$
Answer :
$$y = 2x - 5{x^2}$$
250.
In $$1.0\,s,$$ a particle goes from point $$A$$ to point $$B,$$ moving in a semicircle of radius $$1.0\,m$$ (See Figure). The magnitude of the average velocity is

A
$$3.14\,m/s$$
B
$$2.0\,m/s$$
C
$$1.0\,m/s$$
D
Zero
Answer :
$$2.0\,m/s$$