231. A ball thrown vertically upwards after reaching a maximum height $$h,$$ returns to the starting point after a time of $$10\,s.$$ Its displacement is
A
$$h$$
B
$$2\,h$$
C
$$10\,h$$
D
zero
Answer :
zero
232. Which of the following is correct ?
A
$$\vec A.\vec B \ne \vec B.\vec A$$
B
$$\vec A.\left( {\vec B + \vec C} \right) = A.B + \vec C$$
C
$$\vec A \times \vec B \ne \vec B \times A$$
D
$$\vec A.\left( {\vec B + \vec C} \right) \ne \vec A.\vec B + \vec A.\vec C$$
Answer :
$$\vec A \times \vec B \ne \vec B \times A$$
233. If two balls of masses $${m_1}$$ and $${m_2}\left( {{m_1} = 2{m_2}} \right)$$ are dropped from the same height, then the ratio of the time taken by them to reach the ground will be
A
$${m_1}:{m_2}$$
B
$$2{m_2}:{m_1}$$
C
$$1:1$$
D
$$1:2$$
Answer :
$$1:1$$
234. A hunter tries to hunt a monkey with a small, very poisonous arrow, blown from a pipe with initial speed $${v_0}.$$ The monkey is hanging on a branch of a tree at height $$H$$ above the ground. The hunter is at a distance $$L$$ from the bottom of the tree. The monkey sees the arrow leaving the blow pipe and immediately loses the grip on the tree, falling freely down with zero initial velocity. The minimum initial speed $${v_0}$$ of the arrow for hunter to succeed while monkey is in air is
A
$$\sqrt {\frac{{g\left( {{H^2} + {L^2}} \right)}}{{2H}}} $$
B
$$\sqrt {\frac{{g{H^2}}}{{\sqrt {{H^2} + {L^2}} }}} $$
C
$$\sqrt {\frac{{g\sqrt {{H^2} + {L^2}} }}{H}} $$
D
$$\sqrt {\frac{{2g{H^2}}}{{\sqrt {{H^2} + {L^2}} }}} $$
Answer :
$$\sqrt {\frac{{g\left( {{H^2} + {L^2}} \right)}}{{2H}}} $$
235.
An object, moving with a speed of $$6.25 \,m/s,$$ is decelerated at a rate given by:
$$\frac{{dv}}{{dt}} = - 2.5\sqrt v $$ where $$v$$ is the instantaneous speed. The time taken by the object, to come to rest, would be:
A
$$2 \,s$$
B
$$4 \,s$$
C
$$8 \,s$$
D
$$1 \,s$$
Answer :
$$2 \,s$$
236.
An aircraft moving with a speed of $$250\,m/s$$ is at a height of $$6000\,m,$$ just overhead of an anti aircraft gun. If the muzzle velocity is $$500\,m/s,$$ the firing angle $$q$$ should be:

A
$${30^ \circ }$$
B
$${45^ \circ }$$
C
$${60^ \circ }$$
D
$${75^ \circ }$$
Answer :
$${60^ \circ }$$
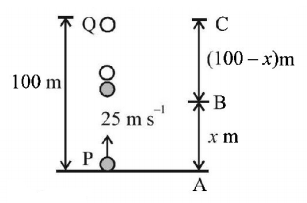
237. A ball is dropped from the top of a tower of height $$100\,m$$ and at the same time another ball is projected vertically upwards from ground with a velocity $$25\,m{s^{ - 1}}.$$ Then the distance from the top of the tower, at which the two balls meet is
A
$$68.4\,m$$
B
$$48.4\,m$$
C
$$18.4\,m$$
D
$$78.4\,m$$
Answer :
$$78.4\,m$$
238. All the graphs below are intended to represent the same motion. One of them does it incorrectly. Pick it up.
A


B


C


D


Answer :


239.
A swimmer wants to cross a river straight. He swim at $$5\,km/hr$$ in still water. A river $$1\,km$$ wide flows at the rate of $$3\,km/hr.$$ Which of the following figure shows the correct direction for the swimmer along which he should strike?
($${V_s} \to $$ velocity of swimmer, $${V_r} \to $$ velocity of river, $$V \to $$ resultant velocity)
A


B


C


D


Answer :


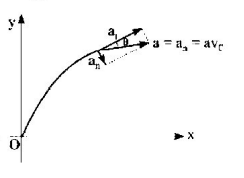
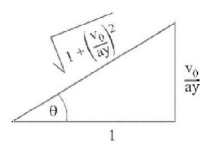
240. A balloon starts rising from the surface of the earth. The ascension rate is constant and equal to $${v_0}.$$ Due to the wind the balloon gathered the horizontal velocity component $${v_x} = ay,$$ where $$a$$ is a constant and $$y$$ is the height of ascent. The tangential, acceleration of the balloon is
A
$$\frac{{{a^2}y}}{{{v_0}}}$$
B
$$\frac{{{a^2}y}}{{\sqrt {1 + {{\left( {\frac{{{a^2}y}}{{{v_0}}}} \right)}^2}} }}$$
C
$$\frac{{{a^2}y}}{{\sqrt {1 + v_0^2} }}$$
D
$$\frac{{{a^2}{v_0}}}{{\sqrt {1 + {{\left( {\frac{{2y}}{a}} \right)}^2}} }}$$
Answer :
$$\frac{{{a^2}y}}{{\sqrt {1 + {{\left( {\frac{{{a^2}y}}{{{v_0}}}} \right)}^2}} }}$$