161. A body $$A$$ begins to move with initial velocity $$2\,m/\sec $$ and continues to move at a constant acceleration $$a.$$ $$\Delta t = $$ 10 seconds after the body $$A$$ begins to move a body $$B$$ departs from the same point with an initial velocity $$12\,m/\sec $$ and moves with the same acceleration $$a.$$ What is the maximum acceleration $$a$$ at which the body $$B$$ can overtake $$A$$ ?
A
$$1\,m/{s^2}$$
B
$$2\,m/{s^2}$$
C
$$\frac{1}{2}\,m/{s^2}$$
D
$$3\,m/{s^2}$$
Answer :
$$1\,m/{s^2}$$
162. A projectile can have the same range $$R$$ for two angles of projection. If $${t_1}$$ and $${t_2}$$ be the times of flight in two cases, then what is the product of two times of flight?
A
$${t_1}{t_2} \propto R$$
B
$${t_1}{t_2} \propto {R^2}$$
C
$${t_1}{t_2} \propto \frac{1}{R}$$
D
$${t_1}{t_2} \propto \frac{1}{{{R^2}}}$$
Answer :
$${t_1}{t_2} \propto R$$
163. Stopping distance of a moving vehicle is directly proportional to
A
square of the initial velocity
B
square of the initial acceleration
C
the initial velocity
D
the initial acceleration
Answer :
square of the initial velocity
164. A particle is moving with a velocity $$\vec v = k\left( {y\hat i + x\hat j} \right)$$ where $$k$$ is a constant. The general equation for its path is:
A
$$y = {x^2} + {\text{ constant}}$$
B
$${y^2} = x + {\text{ constant}}$$
C
$${y^2} = {x^2} + {\text{ constant}}$$
D
$$xy = {\text{ constant}}$$
Answer :
$${y^2} = {x^2} + {\text{ constant}}$$
165. A bullet fired into a wooden block loses half of its velocity after penetrating $$40\,cm.$$ It comes to rest after penetrating a further distance of
A
$$\frac{{22}}{3}cm$$
B
$$\frac{{40}}{3}cm$$
C
$$\frac{{20}}{3}cm$$
D
$$\frac{{22}}{5}cm$$
Answer :
$$\frac{{40}}{3}cm$$
166. A rocket is fired upward from the earth’s surface such that it creates an acceleration of $$19.6\,m{s^{ - 2}}.$$ If after $$5\,s,$$ its engine is switched off, the maximum height of the rocket from earth’s surface would be
A
$$980\,m$$
B
$$735\,m$$
C
$$490\,m$$
D
$$245\,m$$
Answer :
$$735\,m$$
167. A boy standing at the top of a tower of $$20\,m$$ height drops a stone. Assuming, $$g = 10\,m{s^{ - 2}},$$ the velocity with which it hits the ground is
A
$$20\,m/s$$
B
$$40\,m/s$$
C
$$5\,m/s$$
D
$$10\,m/s$$
Answer :
$$20\,m/s$$
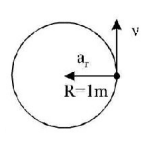
168. A stone tied to the end of a string of $$1\,m$$ long is whirled in a horizontal circle with a constant speed. If the stone makes 22 revolution in 44 seconds, what is the magnitude and direction of acceleration of the stone?
A
$${\pi ^2}m{s^{ - 2}}$$ and direction along the radius towards the centre.
B
$${\pi ^2}m{s^{ - 2}}$$ and direction along the radius away from the centre.
C
$${\pi ^2}m{s^{ - 2}}$$ and direction along the tangent to the circle.
D
$$\frac{{{\pi ^2}}}{4}m{s^{ - 2}}$$ and direction along the radius towards the centre.
Answer :
$${\pi ^2}m{s^{ - 2}}$$ and direction along the radius towards the centre.
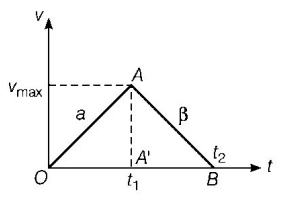
169. A car accelerates from rest at a constant rate $$\alpha $$ for some time, after which it decelerates at a constant rate $$\beta $$ and comes to rest. If the total time elapsed is $$t,$$ then the maximum velocity acquired by the car is
A
$$\left( {\frac{{{\alpha ^2} + {\beta ^2}}}{{\alpha \beta }}} \right)t$$
B
$$\left( {\frac{{{\alpha ^2} - {\beta ^2}}}{{\alpha \beta }}} \right)t$$
C
$$\frac{{\left( {\alpha + \beta } \right)t}}{{\alpha \beta }}$$
D
$$\left( {\frac{{\alpha \beta t}}{{\alpha + \beta }}} \right)$$
Answer :
$$\left( {\frac{{\alpha \beta t}}{{\alpha + \beta }}} \right)$$
170. If a car covers $${\frac{2}{5}^{th}}$$ of the total distance with $${v_1}$$ speed and $${\frac{3}{5}^{th}}$$ distance with $${v_2}$$ then average speed is
A
$$\frac{1}{2}\sqrt {{v_1}{v_2}} $$
B
$$\frac{{{v_1} + {v_2}}}{2}$$
C
$$\frac{{2{v_1}{v_2}}}{{{v_1} + {v_2}}}$$
D
$$\frac{{5{v_1}{v_2}}}{{3{v_1} + 2{v_2}}}$$
Answer :
$$\frac{{5{v_1}{v_2}}}{{3{v_1} + 2{v_2}}}$$