131.
A projectile is fired with a velocity $$v$$ at right angle to the slope which is inclined at an angle $$\theta $$ with the horizontal. The range of the projectile along the inclined plane is:

A
$$\frac{{2{v^2}\tan \theta }}{g}$$
B
$$\frac{{{v^2}\sec \theta }}{g}$$
C
$$\frac{{2{v^2}\tan \theta \sec \theta }}{g}$$
D
$$\frac{{{v^2}\sin \theta }}{g}$$
Answer :
$$\frac{{2{v^2}\tan \theta \sec \theta }}{g}$$
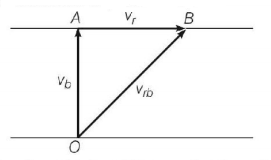
132. A boat is sent across a river with a velocity of $$8\,km\,{h^{ - 1}}.$$ If the resultant velocity of boat is $$10\,km\,{h^{ - 1}},$$ then velocity of river is
A
$$12.8\,km\,{h^{ - 1}}$$
B
$$6\,km\,{h^{ - 1}}$$
C
$$8\,km\,{h^{ - 1}}$$
D
$$10\,km\,{h^{ - 1}}$$
Answer :
$$6\,km\,{h^{ - 1}}$$
133. A particle is moving along a straight line path according to the relation $${s^2} = a{t^2} + 2bt + c\,s$$ represents the distance travelled in $$t$$ seconds and $$a, b, c$$ are constants. Then the acceleration of the particle varies as
A
$${s^{ - 3}}$$
B
$${s^{\frac{3}{2}}}$$
C
$${s^{ - \frac{2}{3}}}$$
D
$${s^2}$$
Answer :
$${s^{ - 3}}$$
134. If the velocity of a particle is $$v = At + B{t^2},$$ where $$A$$ and $$B$$ are constants, then the distance travelled by it between $$1\,s$$ and $$2\,s$$ is
A
$$3A + 7B$$
B
$$\frac{3}{2}A + \frac{7}{3}B$$
C
$$\frac{A}{2} + \frac{B}{3}$$
D
$$\frac{3}{2}A + 4B$$
Answer :
$$\frac{3}{2}A + \frac{7}{3}B$$
135. If the angles of projection of a projectile with same initial velocity exceed or fall short of $${45^ \circ }$$ by equal amounts , then the ratio of horizontal ranges is
A
$$1:2$$
B
$$1:3$$
C
$$1:4$$
D
$$1:1$$
Answer :
$$1:1$$
136. Let two vectors $$\vec A = 3\hat i + \hat j + 2\hat k$$ and $$\vec B = 2\hat i - 2\hat j + 4\hat k.$$ Consider the unit vector perpendicular to both $${\vec A}$$ and $${\vec B}$$ is
A
$$\frac{{\hat i - \hat j - \hat k}}{{\sqrt 3 }}$$
B
$$\frac{{\hat i - \hat j - \hat k}}{{2\sqrt 3 }}$$
C
$$\frac{{ - \hat i - \hat j - \hat k}}{{\sqrt 3 }}$$
D
$$\frac{{ - \hat i - \hat j - \hat k}}{{2\sqrt 3 }}$$
Answer :
$$\frac{{\hat i - \hat j - \hat k}}{{\sqrt 3 }}$$
137. A ball is thrown from a point with a speed $$'{v_0}\,'$$ at an elevation angle of $$\theta .$$ From the same point and at the same instant, a person starts running with a constant speed $$\frac{{'{v_0}\,'}}{2}$$ to catch the ball. Will the person be able to catch the ball ? If yes, what should be the angle of projection $$\theta $$ ?
A
$$No$$
B
$$Yes,{30^ \circ }$$
C
$$Yes,{60^ \circ }$$
D
$$Yes,{45^ \circ }$$
Answer :
$$Yes,{60^ \circ }$$
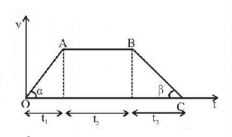
138.
The velocity-time graph of a body is shown in fig. The ratio of average acceleration during the intervals $$OA$$ and $$AB$$ is

A
$$1$$
B
$$\frac{1}{2}$$
C
$$\frac{1}{3}$$
D
$$3$$
Answer :
$$\frac{1}{3}$$
139. A stone released with zero velocity from the top of a tower, reaches the ground in $$4\,s.$$ The height of the tower is $$\left( {g = 10\,m/{s^2}} \right)$$
A
$$20\,m$$
B
$$40\,m$$
C
$$80\,m$$
D
$$160\,m$$
Answer :
$$80\,m$$
140. A car accelerates from rest with a constant acceleration $$\alpha $$ on a straight road. After gaining a velocity $${v_1}$$ the car moves with the same velocity for some-time. Then the car decelerated to rest with a retardation $$\beta .$$ If the total distance covered by the car is equal to $$S,$$ the total time taken for its motion is
A
$$\frac{S}{v} + \frac{v}{2}\left( {\frac{1}{\alpha } + \frac{1}{\beta }} \right)$$
B
$$\frac{S}{v} + \frac{v}{\alpha } + \frac{v}{\beta }$$
C
$$\left( {\frac{v}{\alpha } + \frac{v}{\beta }} \right)$$
D
$$\frac{S}{v} - \frac{v}{2}\left( {\frac{v}{\alpha } + \frac{v}{\beta }} \right)$$
Answer :
$$\frac{S}{v} + \frac{v}{2}\left( {\frac{1}{\alpha } + \frac{1}{\beta }} \right)$$