91. If a car at rest, accelerates uniformly to a speed of $$144\,km/h$$ in $$20\,s,$$ it covers a distance of
A
$$2880\,m$$
B
$$1440\,m$$
C
$$400\,m$$
D
$$20\,m$$
Answer :
$$400\,m$$
92. The velocity of a particle is $$v = {v_0} + gt + f{t^2}.$$ Its position is $$x=0$$ at $$t=0,$$ then its displacement after unit time ($$t=1$$ ) is-
A
$${v_0} + \frac{g}{2} + f$$
B
$${v_0} + 2g + 3f$$
C
$${v_0} + \frac{g}{2} + \frac{f}{3}$$
D
$${v_0} + g + f$$
Answer :
$${v_0} + \frac{g}{2} + \frac{f}{3}$$
93. A boat takes $$2$$ hours to travel $$8\,km$$ and back in still water lake. With water velocity of $$4\,km\,{h^{ - 1}},$$ the time taken for going upstream of $$8\,km$$ and coming back is
A
160 minutes
B
80 minutes
C
100 minutes
D
120 minutes
Answer :
160 minutes
94.
An aircraft executes a horizontal loop of radius $$1.00\,km$$ with a steady speed of $$900\,km/h.$$ The ratio of centripetal acceleration to acceleration due to gravity is
$$\left[ {g = 9.8\,m/{s^2}} \right]$$
A
6.38
B
9.98
C
11.33
D
12.13
Answer :
6.38
95.
Two stones are thrown up simultaneously from the edge of a cliff $$240 \,m$$ high with initial speed of $$10\,m/s$$ and $$40\,m/s$$ respectively. Which of the following graph best represents the time variation of relative position of the second stone with respect to the first?
(Assume stones do not rebound after hitting the ground and neglect air resistance, take $$g = 10\,m/{s^2}$$ )
(The figures are schematic and not drawn to scale)
A


B
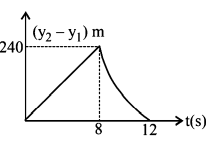

C
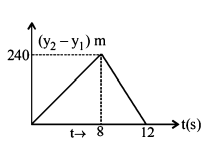

D
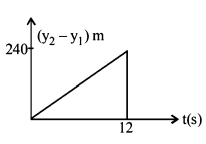

Answer :


96. A particle moves in a straight line with a constant acceleration. It changes its velocity from $$10\,m{s^{ - 1}}$$ to $$20\,m{s^{ - 1}}$$ while passing through a distance $$135\,m$$ in $$t$$ $$\sec.$$ The value of $$t$$ is
A
10
B
1.8
C
12
D
9
Answer :
9
97. If a vector $$2\hat i + 3\hat j + 8\hat k$$ is perpendicular to the vector $$4\hat j - 4\hat i + \alpha \hat k,$$ then the value of $$\alpha $$ is
A
$$ - 1$$
B
$$\frac{1}{2}$$
C
$$ - \frac{1}{2}$$
D
$$1$$
Answer :
$$ - \frac{1}{2}$$
98. A particle is projected at an angle of elevation $$\alpha $$ and after $$t$$ seconds it appears to have an angle of elevation $$\beta $$ as seen from point of projection. The initial velocity will be
A
$$\frac{{gt}}{{2\sin \left( {\alpha - \beta } \right)}}$$
B
$$\frac{{gt\cos \beta }}{{2\sin \left( {\alpha - \beta } \right)}}$$
C
$$\frac{{\sin \left( {\alpha - \beta } \right)}}{{2gt}}$$
D
$$\frac{{2\sin \left( {\alpha - \beta } \right)}}{{gt\cos \beta }}$$
Answer :
$$\frac{{gt\cos \beta }}{{2\sin \left( {\alpha - \beta } \right)}}$$
99. $$\overrightarrow a = 3\hat i - 5\hat j$$ and $$\overrightarrow b = 6\hat i + 3\hat j$$ are two vectors and $$\overrightarrow c $$ is a vector such that $$\overrightarrow c = \overrightarrow a \times \overrightarrow b $$ then $$\left| {\overrightarrow a } \right|:\left| {\overrightarrow b } \right|:\left| {\overrightarrow c } \right|$$
A
$$\sqrt {34} :\sqrt {45} :\sqrt {39} $$
B
$$\sqrt {34} :\sqrt {45} :39$$
C
$$34:39:45$$
D
$$39:35:34$$
Answer :
$$\sqrt {34} :\sqrt {45} :39$$
100. A projectile is given an initial velocity of $$\left( {\hat i + 2\,\hat j} \right)\,m/s,$$ where $${\hat i}$$ is along the ground and $${\hat j}$$ is along the vertical. If $$g = 10\,m/{s^2},$$ the equation of its trajectory is:
A
$$y = x - 5{x^2}$$
B
$$y = 2x - 5{x^2}$$
C
$$4y = 2x - 5{x^2}$$
D
$$4y = 2x - 25{x^2}$$
Answer :
$$y = 2x - 5{x^2}$$