31. Which of the following curves does not represent motion in one dimension?
A


B


C


D


Answer :


32. If $$\overrightarrow A \times \overrightarrow B = \overrightarrow B \times \overrightarrow A ,$$ then the angle between $$A$$ and $$B$$ is-
A
$$\frac{\pi }{2}$$
B
$$\frac{\pi }{3}$$
C
$$\pi $$
D
$$\frac{\pi }{4}$$
Answer :
$$\pi $$
33. A bike accelerates from rest at a constant rate $$5\,m/{s^2}$$ for some time after which it decelerates at a constant rate $$3\,m/{s^2}$$ to come to rest. If the total time elapsed is $$8$$ second, the maximum velocity acquired by the bike is given by
A
$$5\,m/s$$
B
$$10\,m/s$$
C
$$12\,m/s$$
D
$$15\,m/s$$
Answer :
$$15\,m/s$$
34. The condition for $$\vec A + \vec B$$ to be perpendicular to $$\vec A - \vec B$$ is that
A
$$\left| {\vec A} \right| = \left| {\vec B} \right|$$
B
$$\vec A = \vec B$$
C
$$\vec B = 0$$
D
$$\left| {\vec A + \vec B} \right| = \left| {\vec A - \vec B} \right|$$
Answer :
$$\left| {\vec A} \right| = \left| {\vec B} \right|$$
35.
In the given figure, $$a = 15\,m/{s^2}$$ represents the total acceleration of a particle moving in the clockwise direction in a circle of radius $$R = 2.5\,m$$ at a given instant of time. The speed of the particle is

A
$$4.5\,m/s$$
B
$$5.0\,m/s$$
C
$$5.7\,m/s$$
D
$$6.2\,m/s$$
Answer :
$$5.7\,m/s$$
36. A particle starts its motion from rest under the action of a constant force. If the distance covered in first $$10\,s$$ is $${s_1}$$ and that covered in the first $$20\,s$$ is $${s_2},$$ then
A
$${s_2} = 2\,{s_1}$$
B
$${s_2} = 3\,{s_1}$$
C
$${s_2} = 4\,{s_1}$$
D
$${s_2} = {s_1}$$
Answer :
$${s_2} = 4\,{s_1}$$
37.
The position vector of a particle $$R$$ as a function of time is given by
$$R = 4\sin \left( {2\pi t} \right)\hat i + 4\cos \left( {2\pi t} \right)\hat j$$
where $$R$$ is in metre, $$t$$ is in seconds and $${\hat i}$$ and $${\hat j}$$ denote unit vectors along $$x$$ and $$y$$-directions, respectively. Which one of the following statements is wrong for the motion of particle?
A
Acceleration is along $$ - R$$
B
Magnitude of acceleration vector is $$\frac{{{v^2}}}{R},$$ where $$v$$ is the velocity of particle
C
Magnitude of the velocity of particle is $$8\,m/s$$
D
Path of the particle is a circle of radius $$4\,m$$
Answer :
Magnitude of the velocity of particle is $$8\,m/s$$
38.
A boy playing on the roof of a $$10 \,m$$ high building throws a ball with a speed of $$10 \,m/s$$ at an angle of $${30^ \circ }$$ with the horizontal. How far from the throwing point will the ball be at the height of $$10 \,m$$ from the ground?
$$\left[ {g = 10\,m/{s^2},\,\sin 30^\circ = \frac{1}{2},\,\cos {\mkern 1mu} \,30^\circ = \frac{{\sqrt 3 }}{2}} \right]$$
A
$$5.20 \,m$$
B
$$4.33 \,m$$
C
$$2.60 \,m$$
D
$$8.66 \,m$$
Answer :
$$8.66 \,m$$
39.
The velocity of a projectile at the initial point $$A$$ is $$\left( {2\hat i + 3\hat j} \right)m/s.$$ Its velocity (in $$m/s$$ ) at point $$B$$ is

A
$$ - 2\hat i - 3\hat j$$
B
$$ - 2\hat i + 3\hat j$$
C
$$2\hat i - 3\hat j$$
D
$$2\hat i + 3\hat j$$
Answer :
$$2\hat i - 3\hat j$$
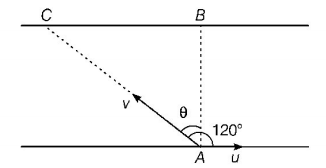
40. A person swims in a river aiming to reach exactly opposite point on the bank of a river. His speed of swimming is $$0.5\,m/s$$ at an angle $${120^ \circ }$$ with the direction of flow of water. The speed of water in stream is
A
$$1.0\,m/s$$
B
$$0.5\,m/s$$
C
$$0.25\,m/s$$
D
$$0.43\,m/s$$
Answer :
$$0.25\,m/s$$