71. A stone falls freely under gravity. It covers distances $${h_1},{h_2}$$ and $${h_3}$$ in the first $$5s,$$ the next $$5s$$ and the next $$5s$$ respectively. The relation between $${h_1},{h_2}$$ and $${h_3}$$ is
A
$${h_1} = 2{h_2} = 3{h_3}$$
B
$${h_1} = \frac{{{h_2}}}{3} = \frac{{{h_3}}}{5}$$
C
$${h_2} = 3{h_1}\,{\text{and}}\,{h_3} = 3{h_2}$$
D
$${h_1} = {h_2} = {h_3}$$
Answer :
$${h_1} = \frac{{{h_2}}}{3} = \frac{{{h_3}}}{5}$$
72. A point traversed half of the distance with a velocity $${v_0}.$$ The half of remaining part of the distance was covered with velocity $${v_1}\& $$ second half of remaining part by $${v_2}$$ velocity. The mean velocity of the point, averaged over the whole time of motion is
A
$$\frac{{{v_0} + {v_1} + {v_2}}}{3}$$
B
$$\frac{{2{v_0} + {v_1} + {v_2}}}{3}$$
C
$$\frac{{{v_0} + 2{v_1} + 2{v_2}}}{3}$$
D
$$\frac{{2{v_0}\left( {{v_1} + {v_2}} \right)}}{{\left( {2{v_0} + {v_1} + {v_2}} \right)}}$$
Answer :
$$\frac{{2{v_0}\left( {{v_1} + {v_2}} \right)}}{{\left( {2{v_0} + {v_1} + {v_2}} \right)}}$$
73. A ball is released from the top of a tower of height $$h$$ meters. It takes $$T$$ seconds to reach the ground. What is the position of the ball at $$\frac{T}{3}$$ second-
A
$$\frac{{8h}}{9}$$ meters from the ground
B
$$\frac{{7h}}{9}$$ meters from the ground
C
$$\frac{{h}}{9}$$ meters from the ground
D
$$\frac{{17h}}{18}$$ meters from the ground
Answer :
$$\frac{{8h}}{9}$$ meters from the ground
74. The length of second’s hand in a watch is $$1\,cm.$$ The change in velocity of its tip in 15 seconds is:
A
zero
B
$$\frac{\pi }{{30\sqrt 2 }}cm/s$$
C
$$\frac{\pi }{{30}}cm/s$$
D
$$\frac{{\pi \sqrt 2 }}{{30}}cm/s$$
Answer :
$$\frac{{\pi \sqrt 2 }}{{30}}cm/s$$
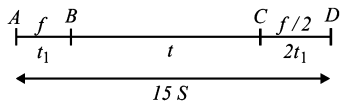
75. A car, starting from rest, accelerates at the rate $$f$$ through a distance $$S,$$ then continues at constant speed for time $$t$$ and then decelerates at the rate $$\frac{f}{2}$$ to come to rest. If the total distance traversed is $$15 \,S ,$$ then-
A
$$S = \frac{1}{6}f{t^2}$$
B
$$S = ft$$
C
$$S = \frac{1}{4}f{t^2}$$
D
$$S = \frac{1}{{72}}f{t^2}$$
Answer :
$$S = \frac{1}{{72}}f{t^2}$$
76. For a particle in uniform circular motion, the acceleration $${\vec a}$$ at a point $$P\left( {R,\theta } \right)$$ on the circle of radius $$R$$ is (Here $$\theta $$ is measured from the x-axis )
A
$$ - \frac{{{v^2}}}{R}\cos \theta \,\hat i + \frac{{{v^2}}}{R}\sin \theta \,\hat j$$
B
$$ - \frac{{{v^2}}}{R}\sin\theta \,\hat i + \frac{{{v^2}}}{R}\cos\theta \,\hat j$$
C
$$ - \frac{{{v^2}}}{R}\cos \theta \,\hat i - \frac{{{v^2}}}{R}\sin \theta \,\hat j$$
D
$$\frac{{{v^2}}}{R}\hat i + \frac{{{v^2}}}{R}\hat j$$
Answer :
$$ - \frac{{{v^2}}}{R}\cos \theta \,\hat i - \frac{{{v^2}}}{R}\sin \theta \,\hat j$$
77.
Two particles $$A$$ and $$B$$ are connected by a rigid rod $$AB.$$ The rod slides along perpendicular rails as shown here. The velocity of $$A$$ to the right is $$10\,m/s.$$ What is the velocity of $$B$$ when angle $$\alpha = {60^ \circ }?$$

A
$$9.8\,m/s$$
B
$$10\,m/s$$
C
$$5.8\,m/s$$
D
$$17.3\,m/s$$
Answer :
$$17.3\,m/s$$
78. Three different objects of masses $${m_1},{m_2}$$ and $${m_3}$$ are allowed to fall from rest and from the same point $$O$$ along three different frictionless paths. The speeds of the three objects on reaching the ground will be in the ratio of
A
$${m_1}:{m_2}:{m_3}$$
B
$${m_1}:2{m_2}:3{m_3}$$
C
$$1:1:1$$
D
$$\frac{1}{{{m_1}}}:\frac{1}{{{m_2}}}:\frac{1}{{{m_3}}}$$
Answer :
$$1:1:1$$
79. A man of height $$h$$ walks in a straight path towards a lamp post of height $$H$$ with velocity $$v.$$ Then velocity of the edge of the shadow on the ground will be
A
$$\frac{{hv}}{{H + h}}$$
B
$$\frac{{Hv}}{{H - h}}$$
C
$$\frac{{H + h}}{{Hv}}$$
D
$$\frac{{\left( {H - h} \right)}}{{Hh}}$$
Answer :
$$\frac{{Hv}}{{H - h}}$$
80.
A particle moves along a straight line $$OX.$$ At a time $$t$$ (in second), the distance $$x$$ (in metre) of the particle from $$O$$ is given by
$$x = 40 + 12t - {t^3}$$
How long would the particle travel before coming to rest?
A
$$24\,m$$
B
$$40\,m$$
C
$$56\,m$$
D
$$16\,m$$
Answer :
$$56\,m$$