21. $$A$$ and $$B$$ are two vectors and $$\theta $$ is the angle between them. If $$\left| {A \times B} \right| = \sqrt 3 \left( {A \cdot B} \right),$$ then the value of $$\theta $$ is
A
$${60^ \circ }$$
B
$${45^ \circ }$$
C
$${30^ \circ }$$
D
$${90^ \circ }$$
Answer :
$${60^ \circ }$$
22. A truck has to carry a load in the shortest time from one station to another station situated at a distance $$L$$ from the first. It can start up or slowdown at the same acceleration or deceleration $$a.$$ What maximum velocity must the truck attain to satisfy this condition?
A
$$\sqrt {La} $$
B
$$\sqrt {2La} $$
C
$$\sqrt {3La} $$
D
$$\sqrt {5La} $$
Answer :
$$\sqrt {La} $$
23.
A man in a row boat must get from point $$A$$ to point $$B$$ on the opposite bank of the river (see figure). The distance $$BC = a.$$ The width of the river $$AC = b.$$ At what minimum speed $$u$$ relative to the still water should the boat travel to reach the point $$B?$$ The velocity of flow of the river is $${v_0}.$$

A
$$\frac{{\sqrt {{a^2} + {b^2}} }}{{{v_0}}}$$
B
$$\frac{{{v_0}b}}{{\sqrt {{a^2} + {b^2}} }}$$
C
$$\frac{{{v_0}a}}{b}$$
D
$$\frac{{{v_0}a}}{a}$$
Answer :
$$\frac{{{v_0}b}}{{\sqrt {{a^2} + {b^2}} }}$$
24. The horizontal range and the maximum height of a projectile are equal. The angle of projection of the projectile is
A
$$\theta = {\tan ^{ - 1}}\left( {\frac{1}{4}} \right)$$
B
$$\theta = {\tan ^{ - 1}}\left( 4 \right)$$
C
$$\theta = {\tan ^{ - 1}}\left( 2 \right)$$
D
$$\theta = {45^ \circ }$$
Answer :
$$\theta = {\tan ^{ - 1}}\left( 4 \right)$$
25. If a car at rest accelerates uniformly to a speed of $$144\,km/h$$ in $$20\,s,$$ it covers a distance of
A
$$2880\,m$$
B
$$1440\,m$$
C
$$400\,m$$
D
$$20\,m$$
Answer :
$$400\,m$$
26. A bus is moving with a velocity of $$10\,m{s^{ - 1}}$$ on a straight road. A scootorist wishes to overtake the bus in one minute. If the bus is at a distance of $$1.2\,km$$ ahead, then the velocity with which he has to chase the bus is
A
$$20\,m{s^{ - 1}}$$
B
$$25\,m{s^{ - 1}}$$
C
$$60\,m{s^{ - 1}}$$
D
$$30\,m{s^{ - 1}}$$
Answer :
$$30\,m{s^{ - 1}}$$
27.
The velocity time graph of the motion of the body is as shown below

The total distance travelled by the body during the motion is equal to _____.
A
$$\frac{1}{2}\left( {AD + BE} \right) \times OC$$
B
$$\frac{1}{2}\left( {OA + BC} \right) \times OC$$
C
$$\frac{1}{2}\left( {OC + AB} \right) \times AD$$
D
$$\frac{1}{2}\left( {OA + AB} \right) \times BC$$
Answer :
$$\frac{1}{2}\left( {OC + AB} \right) \times AD$$
28.
A small particle of mass $$m$$ is projected at an angle $$\theta $$ with the x-axis with an initial velocity $${v_0}$$ in the $$x-y$$ plane as shown in the figure. At a time $$t < \frac{{{v_0}sin\theta }}{g},$$ the angular momentum of the particle is-
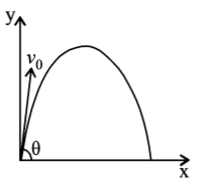
where $$\hat i,\,\hat j$$ and $${\hat k}$$ are unit vectors along $$x, y$$ and $$z$$-axis respectively.
A
$$ - mg\,{v_0}{t^2}\cos \theta \hat j$$
B
$$mg\,{v_0}{t}\cos \theta \,\hat k$$
C
$$ - \frac{1}{2}mg\,{v_0}{t^2}\cos \theta \,\hat k$$
D
$$\frac{1}{2}mg\,{v_0}{t^2}\cos \theta \,\hat i$$
Answer :
$$ - \frac{1}{2}mg\,{v_0}{t^2}\cos \theta \,\hat k$$
29. Let $${\vec a}$$ and $${\vec b}$$ be two unit vectors. If the vectors $$\vec c = \hat a + 2\hat b$$ and $$\vec d = 5\hat a - 4\hat b$$ are perpendicular to each other, then the angle between $${\hat a}$$ and $${\hat b}$$ is:
A
$$\frac{\pi }{6}$$
B
$$\frac{\pi }{2}$$
C
$$\frac{\pi }{3}$$
D
$$\frac{\pi }{4}$$
Answer :
$$\frac{\pi }{3}$$
30.
A ball is dropped from a high rise platform at $$t = 0$$ starting from rest. After $$6\,s,$$ another ball is thrown downwards from the same platform with a speed $$v.$$ The two balls meet at $$t = 18\,s.$$ What is the value of $$v$$ ?
(Take $$g = 10\,m{s^{ - 2}}$$ )
A
$$74\,m{s^{ - 1}}$$
B
$$55\,m{s^{ - 1}}$$
C
$$40\,m{s^{ - 1}}$$
D
$$60\,m{s^{ - 1}}$$
Answer :
$$74\,m{s^{ - 1}}$$