151. The angle between the pair of lines whose equation is $$4{x^2} + 10xy + m{y^2} + 5x + 10y = 0$$ is :
A
$${\tan ^{ - 1}}\frac{3}{8}$$
B
$${\tan ^{ - 1}}\frac{3}{4}$$
C
$${\tan ^{ - 1}}\frac{{2\sqrt {25 - 4m} }}{{m + 4}},\,m\, \in \,R$$
D
none of these
Answer :
$${\tan ^{ - 1}}\frac{3}{4}$$
152. The lines $$p\left( {{p^2} + 1} \right)x - y + q = 0$$ and $${\left( {{p^2} + 1} \right)^2}x + \left( {{p^2} + 1} \right)y + 2q = 0$$ are perpendicular to a common line for :
A
exactly one values of $$p$$
B
exactly two values of $$p$$
C
more than two values of $$p$$
D
no value of $$p$$
Answer :
exactly one values of $$p$$
153. Let $$A\left( {2,\, - 3} \right)$$ and $$B\left( { - 2,\,3} \right)$$ be vertices of a triangle $$ABC.$$ If the centroid of this triangle moves on the line $$2x +3y =1,$$ then the locus of the vertex $$C$$ is the line-
A
$$3x-2y=3$$
B
$$2x-3y=7$$
C
$$3x+2y=5$$
D
$$2x+3y=9$$
Answer :
$$2x+3y=9$$
154. If the line $$2x + y = k$$ passes through the point which divides the line segment joining the points (1, 1) and (2, 4) in the ratio 3 : 2, then $$k$$ equals :
A
$$\frac{{29}}{5}$$
B
5
C
6
D
$$\frac{{11}}{5}$$
Answer :
6
155. The area of the pentagon whose vertices are $$\left( {4,\,1} \right),\,\left( {3,\,6} \right),\,\left( { - 5,\,1} \right),\,\left( { - 3,\, - 3} \right)$$ and $$\left( { - 3,\,0} \right)$$ is :
A
$$30\,{\text{uni}}{{\text{t}}^2}$$
B
$$60\,{\text{uni}}{{\text{t}}^2}$$
C
$$120\,{\text{uni}}{{\text{t}}^2}$$
D
none of these
Answer :
$$30\,{\text{uni}}{{\text{t}}^2}$$
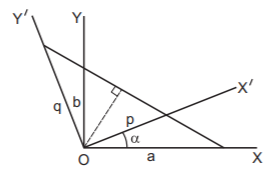
156. A line has intercepts $$a,\,b$$ on the coordinate axes. If the axes are rotated about the origin through an angle $$\alpha $$ then the line has intercepts $$p,\,q$$ on the new position of the axes respectively. Then :
A
$$\frac{1}{{{p^2}}} + \frac{1}{{{q^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{b^2}}}$$
B
$$\frac{1}{{{p^2}}} - \frac{1}{{{q^2}}} = \frac{1}{{{a^2}}} - \frac{1}{{{b^2}}}$$
C
$$\frac{1}{{{p^2}}} + \frac{1}{{{a^2}}} = \frac{1}{{{q^2}}} + \frac{1}{{{b^2}}}$$
D
none of these
Answer :
$$\frac{1}{{{p^2}}} + \frac{1}{{{q^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{b^2}}}$$
157. The locus of variable point whose distance from $$\left( { - 2,\,0} \right)$$ is $$\frac{2}{3}$$ times its distance from the line $$x = - \frac{9}{2}$$ is-
A
ellipse
B
parabola
C
hyperbola
D
none of these
Answer :
ellipse
158. If $$a,\,c,\,b$$ are in GP then the line $$ax+by+c=0$$
A
has a fixed direction
B
always passes through a fixed point
C
forms a triangle with the axes whose area is constant
D
always cuts intercepts on the axes such that their sum is zero
Answer :
forms a triangle with the axes whose area is constant
159. Through the point $$P\left( {\alpha ,\,\beta } \right),$$ where $$\alpha \beta > 0,$$ the straight line $$\frac{x}{a} + \frac{y}{b} = 1$$ is drawn so as to form with axes a triangle of area $$S.$$ If $$ab > 0,$$ then least value of $$S$$ is :
A
$$\alpha \beta $$
B
$$2\alpha \beta $$
C
$$3\alpha \beta $$
D
none of these
Answer :
$$2\alpha \beta $$
160. What is the equation of the line which passes through $$\left( {4,\, - 5} \right)$$ and is perpendicular to $$3x + 4y + 5 = 0\,?$$
A
$$4x - 3y - 31 = 0$$
B
$$3x - 4y - 41 = 0$$
C
$$4x + 3y - 1 = 0$$
D
$$3x + 4y + 8 = 0$$
Answer :
$$4x - 3y - 31 = 0$$