151. If $$\left| z \right| = 1\,\,{\text{and }}\omega = \frac{{z - 1}}{{z + 1}}$$ $$\left( {{\text{where }}z \ne - 1} \right),{\text{then Re}}\left( \omega \right)\,\,{\text{is}}$$
A
$$0$$
B
$$ - \frac{1}{{{{\left| {z + 1} \right|}^2}}}$$
C
$$\left| {\frac{z}{{z + 1}}} \right|.\frac{1}{{{{\left| {z + 1} \right|}^2}}}$$
D
$$\frac{{\sqrt 2 }}{{{{\left| {z + 1} \right|}^2}}}$$
Answer :
$$0$$
152. What is $${\left[ {\frac{{\sin \frac{\pi }{6} + i\left( {1 - \cos \frac{\pi }{6}} \right)}}{{\sin \frac{\pi }{6} - i\left( {1 - \cos \frac{\pi }{6}} \right)}}} \right]^3}$$ where $$i = \sqrt { - 1} ,$$ equal to ?
A
$$1$$
B
$$- 1$$
C
$$i$$
D
$$ - i$$
Answer :
$$i$$
153. If $$\omega$$ is imaginary cube root of unity, then $$\sin \left\{ {\left( {{\omega ^{13}} + {\omega ^2}} \right)\pi + \frac{\pi }{4}} \right\}$$ is equal to
A
$$ - \frac{{\sqrt 3 }}{2}$$
B
$$ - \frac{1}{{\sqrt 2 }}$$
C
$$ \frac{1}{{\sqrt 2 }}$$
D
$$\frac{{\sqrt 3 }}{2}$$
Answer :
$$ - \frac{1}{{\sqrt 2 }}$$
154. If $$z = x + iy$$ satisfies $${\text{amp}}\left( {z - 1} \right) = {\text{amp}}\left( {z + 3i} \right)$$ then the value of $$\left( {x - 1} \right):y$$ is equal to
A
$$2 : 1$$
B
$$1 : 3$$
C
$$- 1 : 3$$
D
None of these
Answer :
$$1 : 3$$
155. If $$z^2 + z +1 = 0,$$ where $$z$$ is complex number, then the value of $${\left( {z + \frac{1}{z}} \right)^2} + {\left( {{z^2} + \frac{1}{{{z^2}}}} \right)^2} + {\left( {{z^3} + \frac{1}{{{z^3}}}} \right)^2} + ..... + {\left( {{z^6} + \frac{1}{{{z^6}}}} \right)^2}\,{\text{is}}$$
A
18
B
54
C
6
D
12
Answer :
12
156. If $$i = \sqrt { - 1} $$ then $$4 + 5{\left( { - \frac{1}{2} + i\frac{{\sqrt 3 }}{2}} \right)^{334}} - 3{\left( {\frac{1}{2} + i\frac{{\sqrt 3 }}{2}} \right)^{365}}$$ is equal to
A
$$1 - i\sqrt 3 $$
B
$$ - 1 + i\sqrt 3 $$
C
$$\sqrt {3}i $$
D
$$ - i\sqrt 3 $$
Answer :
$$\sqrt {3}i $$
157. The complex number $${z_1},{z_2}\,{\text{and }}{z_3}$$ satisfying $$\frac{{{z_1} - {z_3}}}{{{z_2} - {z_3}}} = \frac{{1 - i\sqrt 3 }}{2}$$ are the vertices of a triangle which is
A
of area zero
B
right - angled isosceles
C
equilateral
D
obtuse - angled isosceles
Answer :
equilateral
158. The equation $$z\overline z + \left( {4 - 3i} \right)z + \left( {4 + 3i} \right)\overline z + 5 = 0$$ represents a circle whose radius is
A
$$5$$
B
$$2\sqrt 5 $$
C
$$\frac{5}{2}$$
D
None of these
Answer :
$$2\sqrt 5 $$
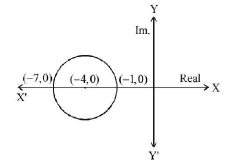
159. If $$\left| {z + 4} \right| \leqslant 3,$$ then the maximum value of $$\left| {z + 1} \right|$$ is
A
6
B
0
C
4
D
10
Answer :
6
160. If $$\omega = \frac{z}{{z - \frac{1}{3}i}}\,{\text{and }}\left| \omega \right| = 1,$$ then $$z$$ lies on
A
an ellipse
B
a circle
C
a straight line
D
a parabola
Answer :
a straight line