131.
If $$z$$ be a complex number satisfying $${z^4} + {z^3} + 2{z^2} + z + 1 = 0$$ then $$\left| z \right|$$ is equal to A
$$\frac{1}{2}$$
B
$$\frac{3}{4}$$
C
$$1$$
D
None of these
Answer :
$$1$$
View Solution
Discuss Question
$$\eqalign{
& {z^4} + {z^3} + {z^2} + {z^2} + z + 1 = 0 \cr
& {\text{or, }}{z^2}\left( {{z^2} + z + 1} \right) + \left( {{z^2} + z + 1} \right) = 0 \cr
& {\text{or, }}\left( {{z^2} + z + 1} \right)\left( {{z^2} + 1} \right) = 0 \cr
& \therefore \,\,z = i, - i,\omega ,{\omega ^2}.\,{\text{For each, }}\left| z \right| = 1. \cr} $$
132.
If $$z$$ in any complex number satisfying $$\left| {z - 1} \right| = 1,$$ then which of the following is correct ? A
$$arg\left( {z - 1} \right) = 2\arg z$$
B
$$2arg\left( z \right) = \frac{2}{3}\arg \left( {{z^2} - z} \right)$$
C
$$arg\left( {z - 1} \right) = \arg \left( {z + 1} \right)$$
D
$$\arg z = 2\arg \left( {z + 1} \right)$$
Answer :
$$arg\left( {z - 1} \right) = 2\arg z$$
View Solution
Discuss Question
$$\eqalign{
& {\text{Since}}\,\left| {z - 1} \right| = 1 \cr
& \therefore \,z - 1 = {e^{i\theta }},\,{\text{where}}\,\,\,\,\arg \left| {z - 1} \right| = \theta \cr
& \therefore \,z = 1 + \cos \,\theta + i\,\sin \,\theta \cr
& = \,2\cos \frac{\theta }{2}\left[ {\cos \frac{\theta }{2} + i\,\sin \,\frac{\theta }{2}} \right] \cr
& = \,2\cos \frac{\theta }{2}.{e^{\frac{{i\theta }}{2}}} = 2{\cos ^2}\frac{\theta }{2} + 2i\,\sin \frac{\theta }{2}\cos \frac{\theta }{2} \cr} $$
133.
If $$\left| {z - 4} \right| < \left| {z - 2} \right|,$$ its solution is given by A
Re$$(z)$$ > 0
B
Re$$(z)$$ < 0
C
Re$$(z)$$ > 3
D
Re$$(z)$$ > 2
Answer :
Re$$(z)$$ > 3
View Solution
Discuss Question
$$\eqalign{
& {\text{Given}}\,\left| {z - 4} \right| < \left| {z - 2} \right|{\text{Let}}\,z = x + iy \cr
& \Rightarrow \,\,\left| {\left( {x - 4} \right) + iy)} \right| < \left| {\left( {x - 2} \right) + iy} \right| \cr
& \Rightarrow \,\,{\left( {x - 4} \right)^2} + {y^2} < {\left( {x - 2} \right)^2} + {y^2} \cr
& \Rightarrow \,\,{x^2} - 8x + 16 < {x^2} - 4x + 4 \cr
& \Rightarrow \,\,12 < 4x \cr
& \Rightarrow \,\,x > 3 \cr} $$
134.
If $$1 + {x^2} = \sqrt {3x} $$ then$$\sum\limits_{n = 1}^{24} {{{\left( {{x^n} - \frac{1}{{{x^n}}}} \right)}^2}} $$ is equal to A
$$48$$
B
$$- 48$$
C
$$ \pm 48\left( {\omega - {\omega ^2}} \right)$$
D
None of these
Answer :
None of these
View Solution
Discuss Question
$$\eqalign{
& 1 - \sqrt 3 x + {x^2} = 0 \cr
& x = \frac{{\sqrt 3 \pm i}}{2} \cr
& x = \frac{{\sqrt 3 + i}}{2} = - i\overline w {\text{ and }}\overline x = \frac{{\sqrt 3 - i}}{2} = iw \cr
& {\text{Now, }}{\left( {{x^n} - \frac{1}{{{x^n}}}} \right)^2} \cr
& = {x^{2n}} + {\overline w ^{2n}} - 2 \cr
& = - {\overline w ^{2n}} - {w^{2n}} - 2 \cr
& = - 2 - \left[ {{{\overline w }^{2n}} + {w^{2n}}} \right] \cr
& {\text{Now, }}\overline w = {w^2}{\text{ and }}1 + w + {w^2} = 0 \cr
& {\text{Hence,}} \cr
& - 2 - \left[ {{{\overline w }^{2n}} + {w^{2n}}} \right] \cr
& = - 2 - \left[ {{w^{4n}} + {w^{2n}}} \right] \cr
& = - 2 - \left[ { - 1} \right] \cr
& = - 2 + 1 \cr
& = - 1 \cr
& {\text{Hence, }}\sum\limits_{n = 1}^{24} {{{\left( {{x^n} - \frac{1}{{{x^n}}}} \right)}^2}} = - 24 \cr} $$
135.
The locus of the center of a circle which touches the circle $$\left| {z - {z_1}} \right| = a\,\,{\text{and }}\left| {z - {z_2}} \right| = b$$ externally $$\left( {z,{z_1}\& {z_2}\,{\text{are complex numbers}}} \right)$$ will be A
an ellipse
B
a hyperbola
C
a circle
D
none of these
Answer :
a hyperbola
View Solution
Discuss Question
Let the circle be $$\left| {z - {z_0}} \right| = r.$$ Then according to given conditions $$\left| {{z_0} - {z_1}} \right| = r + a\,\,{\text{and }}\left| {{z_0} - {z_2}} \right| = r + b.$$ Eliminating $$r,$$ we get $$\left| {{z_0} - {z_1}} \right| - \left| {{z_0} - {z_2}} \right| = a - b.$$
136.
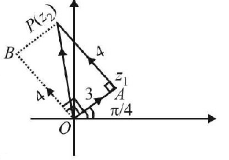
A man walks a distance of 3 units from the origin towards the north-east $$\left( {N{{45}^ \circ }E} \right)$$ direction. From there, he walks a distance of 4 units towards the north-west $$\left( {N{{45}^ \circ }W} \right)$$ direction to reach a point $$P.$$ Then the position of $$P$$ in the Argand plane is A
$$3{e^{i\frac{\pi }{4}}} + 4i$$
B
$$\left( {3 - 4i} \right){e^{i\frac{\pi }{4}}}$$
C
$$\left( {4 + 3i} \right){e^{i\frac{\pi }{4}}}$$
D
$$\left( {3 + 4i} \right){e^{i\frac{\pi }{4}}}$$
Answer :
$$\left( {3 + 4i} \right){e^{i\frac{\pi }{4}}}$$
View Solution
Discuss Question
$$\eqalign{
& \overrightarrow {OP} = \overrightarrow {OA} + \overrightarrow {AP} \cr
& \Rightarrow \,\,\overrightarrow {OP} = \overrightarrow {OA} + \overrightarrow {OB} \cr
& \Rightarrow \,\,\overrightarrow {OP} = 3{e^{i\frac{\pi }{4}}} + 4{e^{i\left( {\frac{\pi }{2} + \frac{\pi }{4}} \right)}} \cr
& = 3{e^{i\frac{\pi }{4}}} + 4{e^{i\frac{\pi }{2}}}.{e^{i\frac{\pi }{4}}} \cr
& = 3{e^{i\frac{\pi }{4}}} + 4i{e^{i\frac{\pi }{4}}} = {e^{i\frac{\pi }{4}}}\left( {3 + 4i} \right). \cr} $$
137.
Non-real complex numbers $$z$$ satisfying the equation $${z^3} + 2{z^2} + 3z + 2 = 0$$ are A
$$\frac{{ - 1 \pm \sqrt { - 7} }}{2}$$
B
$$\frac{{1 + \sqrt {7}i }}{2},\frac{{1 - \sqrt {7}i }}{2}$$
C
$$ - i,\frac{{ - 1 + \sqrt {7}i }}{2},\frac{{ - 1 - \sqrt {7}i }}{2}$$
D
None of these
Answer :
$$\frac{{ - 1 \pm \sqrt { - 7} }}{2}$$
View Solution
Discuss Question
$$\left( {z + 1} \right)\left( {{z^2} + z + 2} \right) = 0;$$ non-real complex roots are found from $${{z^2} + z + 2 = 0}.$$
138.
The value of $$\sum\limits_{k = 1}^{10} {\left( {\sin \frac{{2k\pi }}{{11}} + i\cos \frac{{2k\pi }}{{11}}} \right)} $$ is A
$$i$$
B
$$1$$
C
$$ - 1$$
D
$$ - i$$
Answer :
$$ - i$$
View Solution
Discuss Question
$$\eqalign{
& \sum\limits_{k = 1}^{10} {\left( {\sin \frac{{2k\pi }}{{11}} + i\cos \frac{{2k\pi }}{{11}}} \right)} \cr
& = i\sum\limits_{k = 1}^{10} {\left( {\cos \frac{{2k\pi }}{{11}} - i\sin \frac{{2k\pi }}{{11}}} \right)} \cr
& = i\sum\limits_{k = 1}^{10} {{e^{ - \frac{{2k\pi }}{{11}}i}}} \cr
& = i\left\{ {\sum\limits_{k = 0}^{10} {{e^{ - \frac{{2k\pi }}{{11}}i}} - 1} } \right\} \cr
& = i\left[ {1 + {e^{ - \frac{{2\pi }}{{11}}i}} + {e^{ - \frac{{4\pi }}{{11}}i}} + ..... + 11\,{\text{terms}}} \right] - i \cr
& = i\left[ {\frac{{1 - {{\left( {{e^{ - \frac{{2\pi }}{{11}}}}} \right)}^{11}}}}{{1 - {e^{ - \frac{{2\pi }}{{11}}i}}}}} \right] - i \cr
& = i\left[ {\frac{{1 - {e^{ - 2\pi i}}}}{{1 - {e^{ - \frac{{2\pi }}{{11}}i}}}}} \right] - i \cr
& = i \times 0 - i\,\,\,\,\,\,\,\,\,\,\,\left[ {\because {e^{ - 2\pi i}} = 1} \right] = - i \cr} $$
139.
If $$z = x + iy,{z^{\frac{1}{3}}} = a - ib,$$ then $$\frac{x}{a} - \frac{y}{b} = k\left( {{a^2} - {b^2}} \right)$$ where $$k$$ is equal to A
1
B
2
C
3
D
4
Answer :
4
View Solution
Discuss Question
$$\eqalign{
& {z^{\frac{1}{3}}} = a - ib \cr
& \Rightarrow z = {\left( {a - ib} \right)^3} \cr
& \therefore x + iy = {a^3} + i{b^3} - 3i{a^2}b - 3a{b^2}. \cr
& {\text{Then, }}x = {a^3} - 3a{b^2} \cr
& \Rightarrow \frac{x}{a} = {a^2} - 3{b^2} \cr
& y = {b^3} - 3{a^2}b \cr
& \Rightarrow \frac{y}{b} = {b^2} - 3{a^2} \cr
& {\text{So, }}\frac{x}{a} - \frac{y}{b} = 4\left( {{a^2} - {b^2}} \right) \cr} $$
140.
If $${\log _{\frac{1}{2}}}\frac{{{{\left| z \right|}^2} + 2\left| z \right| + 4}}{{2{{\left| z \right|}^2} + 1}} < 0$$ then the region traced by $$z$$ is A
$$\left| z \right| < 3$$
B
$$1 < \left| z \right| < 3$$
C
$$\left| z \right| > 1$$
D
$$\left| z \right| < 2$$
Answer :
$$\left| z \right| < 3$$
View Solution
Discuss Question
$$\eqalign{
& {\log _{\frac{1}{2}}}\frac{{{{\left| z \right|}^2} + 2\left| z \right| + 4}}{{2{{\left| z \right|}^2} + 1}} < 0 = {\log _{\frac{1}{2}}}1 \cr
& \Rightarrow \,\,\frac{{{{\left| z \right|}^2} + 2\left| z \right| + 4}}{{2{{\left| z \right|}^2} + 1}} > 1 \cr
& {\text{or, }}{\left| z \right|^2} + 2\left| z \right| + 4 > 2{\left| z \right|^2} + 1 \cr
& {\text{or, }}{\left| z \right|^2} - 2\left| z \right| - 3 < 0 \cr
& {\text{or, }}\left( {\left| z \right| + 1} \right)\left( {\left| z \right| - 3} \right) < 0 \cr
& \therefore \,\,\left| z \right| - 3 < 0. \cr} $$