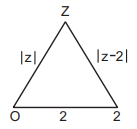121. Let $$z = \frac{{\cos \theta + i\sin \theta }}{{\cos \theta - i\sin \theta }},\frac{\pi }{4} < \theta < \frac{\pi }{2}.$$ Then $$\arg z$$ is
A
$$2\theta $$
B
$$2\theta - \pi $$
C
$$\pi + 2\theta$$
D
None of these
Answer :
$$2\theta $$
122. If $$\omega $$ is a non-real cube root of unity then $$\frac{{1 + 2\omega + 3{\omega ^2}}}{{2 + 3\omega + {\omega ^2}}} + \frac{{2 + 3\omega + {\omega ^2}}}{{3 + \omega + 2{\omega ^2}}}$$ is equal to
A
$$- 1$$
B
$$2\omega $$
C
$$0$$
D
$$ - 2\omega $$
Answer :
$$2\omega $$
123. What is the argument of $$\left( {1 - \sin \theta } \right) + i\,\cos \theta \, ?$$
A
$$\frac{\pi }{2} - \frac{\theta }{2}$$
B
$$\frac{\pi }{2} + \frac{\theta }{2}$$
C
$$\frac{\pi }{4} - \frac{\theta }{2}$$
D
$$\frac{\pi }{4} + \frac{\theta }{2}$$
Answer :
$$\frac{\pi }{4} + \frac{\theta }{2}$$
124. For a complex number $$z,$$ the minimum value of $$\left| z \right| + \left| {z - 2} \right|$$ is
A
1
B
2
C
3
D
None of these
Answer :
2
125. For the complex numbers $$z_1$$ and $$z_2$$ if $${\left| {1 - {{\bar z}_1}{z_2}} \right|^2} - {\left| {{z_1} - {z_2}} \right|^2} = k\left( {1 - {{\left| {{z_1}} \right|}^2}} \right)\left( {1 - {{\left| {{z_2}} \right|}^2}} \right)$$ then $$'k'$$ equals to
A
$$1$$
B
$$- 1$$
C
$$2$$
D
$$- 2$$
Answer :
$$1$$
126. If $$\omega \left( { \ne 1} \right)$$ be a cube root of unity and $${\left( {1 + {\omega ^2}} \right)^n} = {\left( {1 + {\omega ^4}} \right)^n},$$ then the least positive value of $$n$$ is
A
2
B
3
C
5
D
6
Answer :
3
127. The value of $${\left( {1 + i} \right)^3} + {\left( {1 - i} \right)^6}$$ is
A
$$i$$
B
$$2 ( - 1 + 5i)$$
C
$$1 - 5i$$
D
None of these
Answer :
$$2 ( - 1 + 5i)$$
128. If $$z_1, z_2$$ are the roots of the quadratic equation $$az^2 + bz + c = 0$$ such that $$\operatorname{Im} \left( {{z_1},{z_2}} \right) \ne 0$$ then
A
$$a, b, c$$ are all real
B
at least one of $$a, b, c$$ is real
C
at least one of $$a, b, c$$ is imaginary
D
all of $$a, b, c$$ are imaginary
Answer :
at least one of $$a, b, c$$ is imaginary
129. The complex numbers $$z = x+ iy$$ which satisfy the equation $$\left| {\frac{{z - 5i}}{{z + 5i}}} \right| = 1$$ lie on
A
the $$x$$ - axis
B
the straight line $$y = 5$$
C
a circle passing through the origin
D
none of these
Answer :
the $$x$$ - axis
130. Let $$z$$ and $$\omega $$ be two complex numbers such that $$\left| z \right| \leqslant 1,\left| \omega \right| \leqslant 1\,\,{\text{and }}\left| {z + i\omega } \right| = \left| {z - i\bar \omega } \right| = 2.$$ Then $$z$$ equals
A
$$1$$ or $$i$$
B
$$i$$ or $$ - i$$
C
$$1$$ or $$ - i$$
D
$$i$$ or $$ - 1$$
Answer :
$$1$$ or $$ - i$$