Question
$$X$$ and $$Y$$ are two sets and $$f:X \to Y.$$ If $$\left\{ {f\left( c \right) = y;c \subset X,y \subset Y} \right\}$$ and $$\left\{ {{f^{ - 1}}\left( d \right) = x:d \subset Y,x \subset X} \right\},$$ then the true statement is
A.
$$f\left( {{f^{ - 1}}\left( b \right)} \right) = b$$
B.
$${f^{ - 1}}\left( {f\left( a \right)} \right) = a$$
C.
$$f\left( {{f^{ - 1}}\left( b \right)} \right) = b,b \subset y$$
D.
$${f^{ - 1}}\left( {f\left( a \right)} \right) = a,a \subset x$$
Answer :
$${f^{ - 1}}\left( {f\left( a \right)} \right) = a,a \subset x$$
Solution :
Given that $$X$$ and $$Y$$ are two sets and $$f:X \to Y.$$
$$\eqalign{ & \left\{ {f\left( c \right) = y;c \subset X,y \subset Y} \right\}\,{\text{and}} \cr & \left\{ {{f^{ - 1}}\left( d \right) = x:d \subset Y,x \subset X} \right\} \cr} $$
The pictorial representation of given information is as shown:
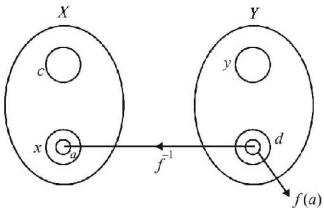
$$\eqalign{ & {\text{Since }}{f^{ - 1}}\left( d \right) = x \Rightarrow f\left( x \right) = d{\text{ Now if }}a \subset x \cr & \Rightarrow f\left( a \right) \subset f\left( x \right) = d \Rightarrow \,{f^{ - 1}}\left[ {f\left( a \right)} \right] = a \cr & \therefore {f^{ - 1}}\left( {f\left( a \right)} \right) = a,a \subset x{\text{ is the correct option}}{\text{.}} \cr} $$
Given that $$X$$ and $$Y$$ are two sets and $$f:X \to Y.$$
$$\eqalign{ & \left\{ {f\left( c \right) = y;c \subset X,y \subset Y} \right\}\,{\text{and}} \cr & \left\{ {{f^{ - 1}}\left( d \right) = x:d \subset Y,x \subset X} \right\} \cr} $$
The pictorial representation of given information is as shown:

$$\eqalign{ & {\text{Since }}{f^{ - 1}}\left( d \right) = x \Rightarrow f\left( x \right) = d{\text{ Now if }}a \subset x \cr & \Rightarrow f\left( a \right) \subset f\left( x \right) = d \Rightarrow \,{f^{ - 1}}\left[ {f\left( a \right)} \right] = a \cr & \therefore {f^{ - 1}}\left( {f\left( a \right)} \right) = a,a \subset x{\text{ is the correct option}}{\text{.}} \cr} $$