Question
What is the area of the parabola $${x^2} = y$$ bounded by the line $$y = 1\,?$$
A.
$$\frac{1}{3}$$ square unit
B.
$$\frac{2}{3}$$ square unit
C.
$$\frac{4}{3}$$ square units
D.
$$2$$ square units
Answer :
$$\frac{4}{3}$$ square units
Solution :
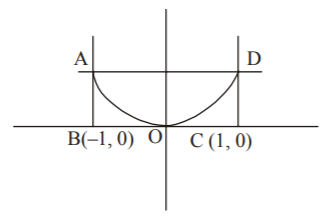
Area of $$ABCD = 2 \times 1 = 2\,{\text{sq}}{\text{. units}}$$
Area of $$BAODC = \int_{ - 1}^1 {{x^2}dx} = \left. {\frac{{{x^3}}}{3}} \right|_{ - 1}^1 = \frac{2}{3}\,{\text{sq}}{\text{. units}}$$
Required area $$ = 2 - \frac{2}{3} = \frac{4}{3}{\text{ sq}}{\text{. units}}$$

Area of $$ABCD = 2 \times 1 = 2\,{\text{sq}}{\text{. units}}$$
Area of $$BAODC = \int_{ - 1}^1 {{x^2}dx} = \left. {\frac{{{x^3}}}{3}} \right|_{ - 1}^1 = \frac{2}{3}\,{\text{sq}}{\text{. units}}$$
Required area $$ = 2 - \frac{2}{3} = \frac{4}{3}{\text{ sq}}{\text{. units}}$$