Question
Two vertices of an equilateral triangle are $$\left( { - 1,\,0} \right)$$ and $$\left( {1,\,0} \right)$$ and its third vertex lies above the $$x$$-axis. The equation of the circumcircle of the triangle is :
A.
$${x^2} + {y^2} = 1$$
B.
$$\sqrt 3 \left( {{x^2} + {y^2}} \right) + 2y - \sqrt 3 = 0$$
C.
$$\sqrt 3 \left( {{x^2} + {y^2}} \right) - 2y - \sqrt 3 = 0$$
D.
none of these
Answer :
$$\sqrt 3 \left( {{x^2} + {y^2}} \right) - 2y - \sqrt 3 = 0$$
Solution :
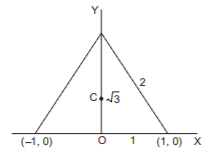
The circumcentre $$C$$ is the centroid for an equilateral triangle.
$$\therefore \,C = \left( {0,\,\frac{1}{{\sqrt 3 }}} \right)$$ and radius $$ = \frac{2}{3}.\sqrt 3 .$$
So, the circumcircle is $${\left( {x - 0} \right)^2} + {\left( {y - \frac{1}{{\sqrt 3 }}} \right)^2} = {\left( {\frac{2}{3}.\sqrt 3 } \right)^2}$$

The circumcentre $$C$$ is the centroid for an equilateral triangle.
$$\therefore \,C = \left( {0,\,\frac{1}{{\sqrt 3 }}} \right)$$ and radius $$ = \frac{2}{3}.\sqrt 3 .$$
So, the circumcircle is $${\left( {x - 0} \right)^2} + {\left( {y - \frac{1}{{\sqrt 3 }}} \right)^2} = {\left( {\frac{2}{3}.\sqrt 3 } \right)^2}$$