Question
Two sets $$A$$ and $$B$$ are as under :
Two sets $$A$$ and $$B$$ are as under :
$$\eqalign{
& A = \left\{ {\left( {a,\,b} \right) \in R \times R:\left| {a - 5} \right| < 1{\text{ and }}\left| {b - 5} \right| < 1} \right\}; \cr
& B = \left\{ {\left( {a,\,b} \right) \in R \times R:4{{\left( {a - 6} \right)}^2} + 9{{\left( {b - 5} \right)}^2} \leqslant 36} \right\}. \cr} $$
Then :
A.
$$A \subset B$$
B.
$$A \cap B = \phi \,\,\left( {{\text{an empty set}}} \right)$$
C.
$${\text{neither }}A \subset B{\text{ nor }}B \subset A$$
D.
$$B \subset A$$
Answer :
$$A \subset B$$
Solution :
$$A = \left\{ {\left( {a,\,b} \right) \in R \times R:\left| {a - 5} \right| < 1,{\text{ }}\left| {b - 5} \right| < 1} \right\}$$
Let $$a-5=x, \,\,b-5=y$$
Set $$A$$ contains all points inside $$\left| x \right| < 1,\,\left| y \right| < 1$$
$$B = \left\{ {\left( {a,\,b} \right) \in R \times R:4{{\left( {a - 6} \right)}^2} + 9{{\left( {b - 5} \right)}^2} \leqslant 36} \right\}$$
Set $$B$$ contains all points inside or on
$$\frac{{{{\left( {x - 1} \right)}^2}}}{9} + \frac{{{y^2}}}{4} = 1$$
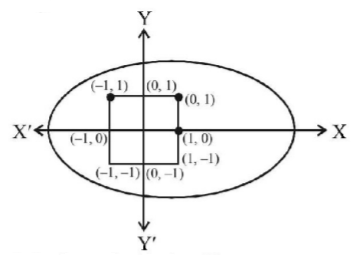
$$\therefore \left( { \pm 1,\, \pm 1} \right)$$ lies inside the ellipse.
Hence, $$A \subset B$$
$$A = \left\{ {\left( {a,\,b} \right) \in R \times R:\left| {a - 5} \right| < 1,{\text{ }}\left| {b - 5} \right| < 1} \right\}$$
Let $$a-5=x, \,\,b-5=y$$
Set $$A$$ contains all points inside $$\left| x \right| < 1,\,\left| y \right| < 1$$
$$B = \left\{ {\left( {a,\,b} \right) \in R \times R:4{{\left( {a - 6} \right)}^2} + 9{{\left( {b - 5} \right)}^2} \leqslant 36} \right\}$$
Set $$B$$ contains all points inside or on
$$\frac{{{{\left( {x - 1} \right)}^2}}}{9} + \frac{{{y^2}}}{4} = 1$$

$$\therefore \left( { \pm 1,\, \pm 1} \right)$$ lies inside the ellipse.
Hence, $$A \subset B$$