Question
Two angles of a triangle are $$\frac{\pi }{6}$$ and $$\frac{\pi }{4},$$ and the length of the included side is $$\left( {\sqrt 3 + 1} \right)\,cm.$$ The area of the triangle is
A.
$$\frac{{\sqrt 3 - 1}}{2}\,{cm^2}$$
B.
$$\frac{{\sqrt 3}}{2}\,{cm^2}$$
C.
$$\frac{{\sqrt 3 + 1}}{2}\,{cm^2}$$
D.
None of these
Answer :
$$\frac{{\sqrt 3 + 1}}{2}\,{cm^2}$$
Solution :
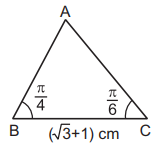
$$\eqalign{ & A = \pi - \frac{\pi }{4} - \frac{\pi }{6} = {105^ \circ }. \cr & {\text{So, }}\frac{{\sqrt 3 + 1}}{{\sin {{105}^ \circ }}} = \frac{c}{{\sin \frac{\pi }{6}}} \cr & \Rightarrow \,\,c = \frac{{\frac{{\sqrt 3 + 1}}{2}}}{{\frac{{\sqrt 3 + 1}}{{2\sqrt 2 }}}} = \sqrt 2 \cr & \therefore \,\,{\text{area}} = \frac{1}{2}ac\sin B = \frac{1}{2} \cdot \left( {\sqrt 3 + 1} \right)\sqrt 2 \cdot \sin \frac{\pi }{4}. \cr} $$

$$\eqalign{ & A = \pi - \frac{\pi }{4} - \frac{\pi }{6} = {105^ \circ }. \cr & {\text{So, }}\frac{{\sqrt 3 + 1}}{{\sin {{105}^ \circ }}} = \frac{c}{{\sin \frac{\pi }{6}}} \cr & \Rightarrow \,\,c = \frac{{\frac{{\sqrt 3 + 1}}{2}}}{{\frac{{\sqrt 3 + 1}}{{2\sqrt 2 }}}} = \sqrt 2 \cr & \therefore \,\,{\text{area}} = \frac{1}{2}ac\sin B = \frac{1}{2} \cdot \left( {\sqrt 3 + 1} \right)\sqrt 2 \cdot \sin \frac{\pi }{4}. \cr} $$