The value of $$'x'$$ for which the angle between the vectors $$\overrightarrow a = 2{x^2}\hat i + 4x\hat j + \hat k$$     and $$\overrightarrow b = 7\hat i - 2\hat j + x\hat k$$     is obtuse are :

Solution :

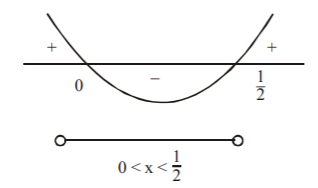
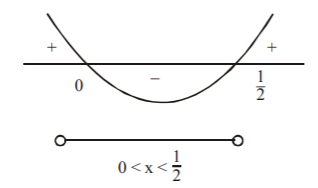
$$\eqalign{ & \overrightarrow a .\overrightarrow b = \left( {2{x^2}\hat i + 4x\hat j + \hat k} \right).\left( {7\hat i - 2\hat j + x\hat k} \right) \cr & \Rightarrow \overrightarrow a .\overrightarrow b = 2{x^2}\left( 7 \right) + \left( {4x} \right)\left( { - 2} \right) + \left( 1 \right)\left( x \right) \cr & \Rightarrow \overrightarrow a .\overrightarrow b = 14{x^2} - 7x \cr & \hat i.\hat i = 1s = \hat j.\hat j = 1 \cr} $$
The angle between vectors $$\overrightarrow a $$ and $$\overrightarrow b $$ is obtuse
$$\eqalign{ & \Rightarrow \overrightarrow a .\overrightarrow b < 0 \cr & \Rightarrow 14{x^2} - 7x < 0 \cr & \Rightarrow 7x\left( {2x - 1} \right) < 0 \cr & \Rightarrow 14x\left( {x - \frac{1}{2}} \right) < 0 \cr} $$
$$ \Rightarrow x$$  lies between $$0$$ and $$\frac{1}{2}$$ (By the Method of Intervals) i.e., $$0 < x < \frac{1}{2}$$
Hence, the angle between the given vectors is obtuse if $$x\, \in \left( {0,\,\frac{1}{2}} \right).$$