Question
The upper $${\frac{3}{4}^{th}}$$ portion of a vertical pole subtends an angle $${\tan ^{ - 1}}\frac{3}{5}$$ at a point in the horizontal plane through its foot and at a distance $$40\,m$$ from the foot. A possible height of the vertical pole is :
A.
$$80\,m$$
B.
$$20\,m$$
C.
$$40\,m$$
D.
$$60\,m$$
Answer :
$$40\,m$$
Solution :
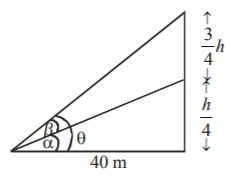
$$\eqalign{ & \theta = \alpha + \beta ,\,\beta = {\tan ^{ - 1}}\left( {\frac{3}{5}} \right){\text{ or }}\beta = \theta - \alpha \cr & \Rightarrow \tan \,\beta = \frac{{\tan \,\theta - \tan \,\alpha }}{{1 + \tan \,\theta .\tan \,\alpha }} \cr & {\text{or }}\frac{3}{5} = \frac{{\frac{h}{{40}} - \frac{h}{{160}}}}{{1 + \frac{h}{{40}}.\frac{h}{{160}}}} \cr & \Rightarrow {h^2} - 200h + 6400 = 0 \cr & \Rightarrow h = 40{\text{ or }}160{\text{ metre}} \cr & \therefore \,{\text{possible height}} = 40\,{\text{metre}} \cr} $$

$$\eqalign{ & \theta = \alpha + \beta ,\,\beta = {\tan ^{ - 1}}\left( {\frac{3}{5}} \right){\text{ or }}\beta = \theta - \alpha \cr & \Rightarrow \tan \,\beta = \frac{{\tan \,\theta - \tan \,\alpha }}{{1 + \tan \,\theta .\tan \,\alpha }} \cr & {\text{or }}\frac{3}{5} = \frac{{\frac{h}{{40}} - \frac{h}{{160}}}}{{1 + \frac{h}{{40}}.\frac{h}{{160}}}} \cr & \Rightarrow {h^2} - 200h + 6400 = 0 \cr & \Rightarrow h = 40{\text{ or }}160{\text{ metre}} \cr & \therefore \,{\text{possible height}} = 40\,{\text{metre}} \cr} $$