Question
The sum of the radii of inscribed and circumscribed circles for an $$n$$ sided regular polygon of side $$a,$$ is
A.
$$\frac{a}{4}\cot \left( {\frac{\pi }{{2n}}} \right)$$
B.
$$a\cot \left( {\frac{\pi }{{n}}} \right)$$
C.
$$\frac{a}{2}\cot \left( {\frac{\pi }{{2n}}} \right)$$
D.
$$a\cot \left( {\frac{\pi }{{2n}}} \right)$$
Answer :
$$\frac{a}{2}\cot \left( {\frac{\pi }{{2n}}} \right)$$
Solution :
$$\eqalign{ & \tan \left( {\frac{\pi }{4}} \right) = \frac{a}{{2r}};\sin \left( {\frac{\pi }{n}} \right) = \frac{a}{{2R}} \cr & r + R = \frac{a}{2}\left[ {\cot \frac{\pi }{n} + {\text{cosec}}\frac{\pi }{n}} \right] \cr} $$
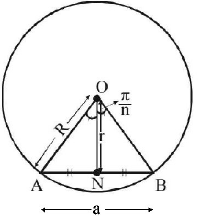
$$\eqalign{ & = \frac{a}{2}\left[ {\frac{{\cos \frac{\pi }{n} + 1}}{{\sin \frac{\pi }{n}}}} \right] \cr & = \frac{a}{2}\left[ {\frac{{2{{\cos }^2}\frac{\pi }{{2n}}}}{{2\sin \frac{\pi }{{2n}}\cos \frac{\pi }{{2n}}}}} \right] \cr & = \frac{a}{2}\cot \frac{\pi }{{2\pi }} \cr} $$
$$\eqalign{ & \tan \left( {\frac{\pi }{4}} \right) = \frac{a}{{2r}};\sin \left( {\frac{\pi }{n}} \right) = \frac{a}{{2R}} \cr & r + R = \frac{a}{2}\left[ {\cot \frac{\pi }{n} + {\text{cosec}}\frac{\pi }{n}} \right] \cr} $$

$$\eqalign{ & = \frac{a}{2}\left[ {\frac{{\cos \frac{\pi }{n} + 1}}{{\sin \frac{\pi }{n}}}} \right] \cr & = \frac{a}{2}\left[ {\frac{{2{{\cos }^2}\frac{\pi }{{2n}}}}{{2\sin \frac{\pi }{{2n}}\cos \frac{\pi }{{2n}}}}} \right] \cr & = \frac{a}{2}\cot \frac{\pi }{{2\pi }} \cr} $$