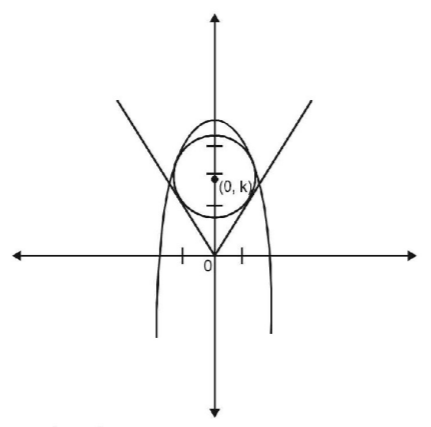
The radius of a circle, having minimum area, which touches the curve $$y = 4 - {x^2}$$  and the lines, $$y = \left| x \right|$$  is :

Solution :
Let the equation of circle be
$${x^2} + {\left( {y - k} \right)^2} = {r^2}$$
It touches $$x-y=0$$

$$\eqalign{ & \Rightarrow \left| {\frac{{0 - k}}{{\sqrt 2 }}} \right| = r \cr & \Rightarrow k = r\sqrt 2 \cr} $$
$$\therefore $$ Equation of circle becomes
$${x^2} + {\left( {y - k} \right)^2} = \frac{{{k^2}}}{2}.....({\text{i}})$$
It touches $$y = 4 - {x^2}$$   as well
$$\therefore $$ Solving the two equations
$$\eqalign{ & \Rightarrow 4 - y + {\left( {y - k} \right)^2} = \frac{{{k^2}}}{2} \cr & \Rightarrow {y^2} - y\left( {2k + 1} \right) + \frac{{{k^2}}}{2} + 4 = 0 \cr} $$
It will give equal roots $$\therefore $$ $$D=0$$
$$\eqalign{ & \Rightarrow {\left( {2k + 1} \right)^2} = 4\left( {\frac{{{k^2}}}{2} + 4} \right) \cr & \Rightarrow 2{k^2} + 4k - 15 = 0 \cr & \Rightarrow k = \frac{{ - 2 + \sqrt {34} }}{2} \cr & \therefore r = \frac{k}{{\sqrt 2 }} = \frac{{ - 2 + \sqrt {34} }}{{2\sqrt 2 }} \cr} $$