Question
The parabolas $${y^2} = 4x$$ and $${x^2} = 4y$$ divide the square region bounded by the lines $$x = 4,\,y = 4$$ and the coordinate axes. If $${S_1},\,{S_2},\,{S_3}$$ are respectively the areas of these parts numbered from top to bottom; then $${S_1}:{S_2}:{S_3}$$ is-
A.
$$1 : 2 : 1$$
B.
$$1 : 2 : 3$$
C.
$$2 : 1 : 2$$
D.
$$1 : 1 : 1$$
Answer :
$$1 : 1 : 1$$
Solution :
Intersection points of $${x^2} = 4y$$ and $${y^2} = 4x$$ are $$\left( {0,\,0} \right)$$ and $$\left( {4,\,4} \right).$$ The graph is as shown in the figure.
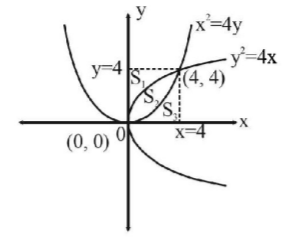
By symmetry, we observe
$$\eqalign{ & {S_1} = {S_3} = \int\limits_0^4 {y\,dx} = \int\limits_0^4 {\frac{{{x^2}}}{4}dx} = \left[ {\frac{{{x^3}}}{{12}}} \right]_0^4 = \frac{{16}}{3}\,\,{\text{sq}}{\text{.}}\,{\text{units}} \cr & {\text{Also }}{S_2} = \int\limits_0^4 {\left( {2\sqrt x - \frac{{{x^2}}}{4}} \right)dx} = \left[ {\frac{{2{x^{\frac{3}{2}}}}}{{\frac{3}{2}}} - \frac{{{x^3}}}{{12}}} \right]_0^4 \cr & = \frac{4}{3} \times 8 - \frac{{16}}{3} = \frac{{16}}{3}\,\,{\text{sq}}{\text{.}}\,{\text{units}} \cr & \therefore {S_1}:{S_2}:{S_3} = 1:1:1 \cr} $$
Intersection points of $${x^2} = 4y$$ and $${y^2} = 4x$$ are $$\left( {0,\,0} \right)$$ and $$\left( {4,\,4} \right).$$ The graph is as shown in the figure.

By symmetry, we observe
$$\eqalign{ & {S_1} = {S_3} = \int\limits_0^4 {y\,dx} = \int\limits_0^4 {\frac{{{x^2}}}{4}dx} = \left[ {\frac{{{x^3}}}{{12}}} \right]_0^4 = \frac{{16}}{3}\,\,{\text{sq}}{\text{.}}\,{\text{units}} \cr & {\text{Also }}{S_2} = \int\limits_0^4 {\left( {2\sqrt x - \frac{{{x^2}}}{4}} \right)dx} = \left[ {\frac{{2{x^{\frac{3}{2}}}}}{{\frac{3}{2}}} - \frac{{{x^3}}}{{12}}} \right]_0^4 \cr & = \frac{4}{3} \times 8 - \frac{{16}}{3} = \frac{{16}}{3}\,\,{\text{sq}}{\text{.}}\,{\text{units}} \cr & \therefore {S_1}:{S_2}:{S_3} = 1:1:1 \cr} $$