Question
The number of real solutions of $$\left( {x,y} \right),$$ where $$\left| y \right| = \sin x,y = {\cos ^{ - 1}}\left( {\cos x} \right), - 2\pi \leqslant x \leqslant 2\pi ,$$ is
A.
2
B.
1
C.
3
D.
4
Answer :
3
Solution :
$$\eqalign{ & {\text{In }}\left[ {0,\pi } \right],\left| y \right| = \sin x,y = {\cos ^{ - 1}}\left( {\cos x} \right) = x. \cr & {\text{In }}\left[ {\pi ,2\pi } \right],\left| y \right| = \sin x,y = {\cos ^{ - 1}}\left\{ {\cos \left( {2\pi - x} \right)} \right\} = 2\pi - x. \cr & {\text{In }}\left[ { - \pi ,0} \right],\left| y \right| = \sin x,y = {\cos ^{ - 1}}\left\{ {\cos \left( { - x} \right)} \right\} = - x. \cr & {\text{In }}\left[ { - 2\pi , - \pi } \right],\left| y \right| = \sin x,y = {\cos ^{ - 1}}\left\{ {\cos \left( {2\pi + x} \right)} \right\} = 2\pi + x. \cr} $$
Plotting the graphs, we have,
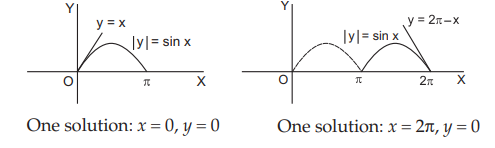
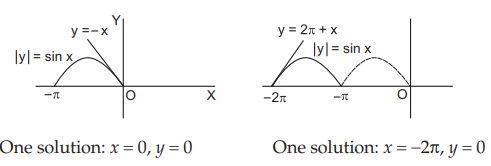
∴ there are 3 solutions $$\left( {0,0} \right),\left( {2\pi ,0} \right),\left( { - 2\pi ,0} \right).$$
$$\eqalign{ & {\text{In }}\left[ {0,\pi } \right],\left| y \right| = \sin x,y = {\cos ^{ - 1}}\left( {\cos x} \right) = x. \cr & {\text{In }}\left[ {\pi ,2\pi } \right],\left| y \right| = \sin x,y = {\cos ^{ - 1}}\left\{ {\cos \left( {2\pi - x} \right)} \right\} = 2\pi - x. \cr & {\text{In }}\left[ { - \pi ,0} \right],\left| y \right| = \sin x,y = {\cos ^{ - 1}}\left\{ {\cos \left( { - x} \right)} \right\} = - x. \cr & {\text{In }}\left[ { - 2\pi , - \pi } \right],\left| y \right| = \sin x,y = {\cos ^{ - 1}}\left\{ {\cos \left( {2\pi + x} \right)} \right\} = 2\pi + x. \cr} $$
Plotting the graphs, we have,
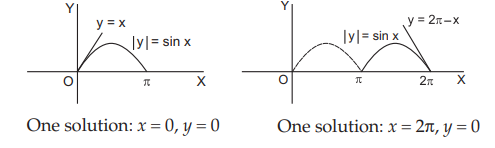
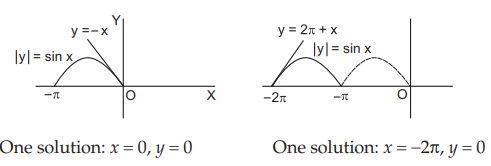
∴ there are 3 solutions $$\left( {0,0} \right),\left( {2\pi ,0} \right),\left( { - 2\pi ,0} \right).$$