Question
The number of real solutions of the equation $$\sqrt {1 + \cos 2x} = \sqrt 2 \,{\sin ^{ - 1}}\left( {\sin x} \right), - \pi \leqslant x \leqslant \pi ,$$ is
A.
0
B.
1
C.
2
D.
infinite
Answer :
2
Solution :
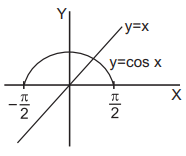
Here, $$\left| {\cos x} \right| = {\sin ^{ - 1}}\left( {\sin x} \right).$$
If, $$ - \frac{\pi }{2} \leqslant x \leqslant \frac{\pi }{2}\,{\text{then}}\,\,\cos x = x.$$
In the case there is one solution, obtained graphically.
If, $$\frac{\pi }{2} < x \leqslant \pi $$ then $$ - \cos x = {\sin ^{ - 1}}\left\{ {\sin \left( {\pi - x} \right)} \right\} = \pi - x.$$
$$\therefore \,\,\cos x = x - \pi .$$
In this case there is one solution, obtained graphically.
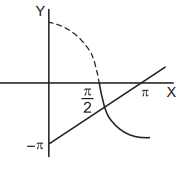
If, $$ - \pi \leqslant x < - \frac{\pi }{2}$$ then $$ - \cos x = {\sin ^{ - 1}}\left\{ {\sin \left( { - \pi - x} \right)} \right\} = - x - \pi ,\,{\text{i}}{\text{.e}}{\text{.,}}\cos x = x + \pi .$$
This gives no solution as can be seen from their graphs.
Here, $$\left| {\cos x} \right| = {\sin ^{ - 1}}\left( {\sin x} \right).$$
If, $$ - \frac{\pi }{2} \leqslant x \leqslant \frac{\pi }{2}\,{\text{then}}\,\,\cos x = x.$$
In the case there is one solution, obtained graphically.

If, $$\frac{\pi }{2} < x \leqslant \pi $$ then $$ - \cos x = {\sin ^{ - 1}}\left\{ {\sin \left( {\pi - x} \right)} \right\} = \pi - x.$$
$$\therefore \,\,\cos x = x - \pi .$$
In this case there is one solution, obtained graphically.

If, $$ - \pi \leqslant x < - \frac{\pi }{2}$$ then $$ - \cos x = {\sin ^{ - 1}}\left\{ {\sin \left( { - \pi - x} \right)} \right\} = - x - \pi ,\,{\text{i}}{\text{.e}}{\text{.,}}\cos x = x + \pi .$$
This gives no solution as can be seen from their graphs.