The maximum volume (in $$cu.m$$  ) of the right circular cone having slant height $$3\,m$$  is:

Solution :


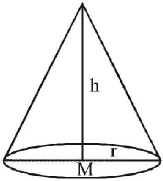
$$\eqalign{ & {h^2} + {r^2} = { \approx ^2} = 9\,......\left( 1 \right) \cr & {\text{Volume}}\,{\text{of}}\,{\text{cone}} \cr & V = \frac{1}{3}\pi {r^2}h\,......\left( 2 \right) \cr & {\text{From }}\left( {\text{1}} \right){\text{ and }}\left( {\text{2}} \right){\text{,}} \cr & \Rightarrow V = \frac{1}{3}\pi \left( {9 - {h^2}} \right)h \Rightarrow V = \frac{1}{3}\pi \left( {9h - {h^3}} \right) \cr & \Rightarrow \frac{{dv}}{{dh}} = \frac{1}{3}\pi \left( {9 - 3{h^2}} \right) \cr & {\text{For}}\,{\text{maxima/minima,}} \cr & \frac{{dV}}{{dh}} = 0 \Rightarrow \frac{1}{3}\pi \left( {9 - 3{h^2}} \right) = 0 \cr & \Rightarrow h = \pm \sqrt 3 \Rightarrow h = \sqrt 3 \cr & {\text{Now}}\,;\frac{{{d^2}V}}{{d{h^2}}} = \frac{1}{3}\pi \left( { - 6h} \right) \cr & {\text{Here}},\,{\left( {\frac{{{d^2}V}}{{d{h^2}}}} \right)_{{\text{at}}\,h = \sqrt 3 }} < 0 \cr & {\text{Then,}}\,h = \sqrt 3 \,{\text{is point of maxima}} \cr & {\text{Hence, the required maximum volume is,}} \cr & V = \frac{1}{3}\pi \left( {9 - 3} \right)\sqrt 3 = 2\sqrt 3 \pi \cr} $$