Question
The locus of the mid-point of the chord of contact of tangents drawn from points lying on the straight line $$4x - 5y = 20$$ to the circle $${x^2} + {y^2} = 9$$ is-
A.
$$20\left( {{x^2} + {y^2}} \right) - 36x + 45y = 0$$
B.
$$20\left( {{x^2} + {y^2}} \right) + 36x - 45y = 0$$
C.
$$36\left( {{x^2} + {y^2}} \right) - 20x + 45y = 0$$
D.
$$36\left( {{x^2} + {y^2}} \right) + 20x - 45y = 0$$
Answer :
$$20\left( {{x^2} + {y^2}} \right) - 36x + 45y = 0$$
Solution :
Any point $$P$$ on line $$4x-5y =20$$ is $$\left( {\alpha ,\,\frac{{4\alpha - 20}}{5}} \right).$$
Equation of chord of contact $$AB$$ to the circle $${x^2} + {y^2} = 9$$
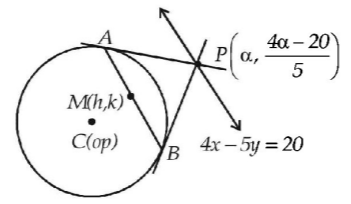
drawn from point $$P\left( {\alpha ,\,\frac{{4\alpha - 20}}{5}} \right)$$ is
$$x.\alpha + y.\left( {\frac{{4\alpha - 20}}{5}} \right) = 9.....(1)$$
Also the equation of chord $$AB$$ whose mid point is $$\left( {h,\,k} \right)$$ is
$$hx + ky = {h^2} + {k^2}.....(2)$$
$$\because $$ Equations (1) and (2) represent the same line, therefore
$$\eqalign{ & \frac{h}{\alpha } = \frac{k}{{\frac{{4\alpha - 20}}{5}}} = \frac{{{h^2} + {k^2}}}{9} \cr & \Rightarrow 5k\alpha = 4h\alpha - 20h{\text{ and }}9h = \alpha \left( {{h^2} + {k^2}} \right) \cr & \Rightarrow \alpha = \frac{{20h}}{{4h - 5k}}{\text{ and }}\alpha = \frac{{9h}}{{{h^2} + {k^2}}} \cr & \Rightarrow \frac{{20h}}{{4h - 5k}} = \frac{{9h}}{{{h^2} + {k^2}}} \cr & \Rightarrow 20\left( {{h^2} + {k^2}} \right) = 9\left( {4h - 5k} \right) \cr} $$
$$\therefore $$ Locus of $$\left( {h,\,k} \right)$$
$$20\left( {{x^2} + {y^2}} \right) - 36x + 45y = 0$$
Any point $$P$$ on line $$4x-5y =20$$ is $$\left( {\alpha ,\,\frac{{4\alpha - 20}}{5}} \right).$$
Equation of chord of contact $$AB$$ to the circle $${x^2} + {y^2} = 9$$

drawn from point $$P\left( {\alpha ,\,\frac{{4\alpha - 20}}{5}} \right)$$ is
$$x.\alpha + y.\left( {\frac{{4\alpha - 20}}{5}} \right) = 9.....(1)$$
Also the equation of chord $$AB$$ whose mid point is $$\left( {h,\,k} \right)$$ is
$$hx + ky = {h^2} + {k^2}.....(2)$$
$$\because $$ Equations (1) and (2) represent the same line, therefore
$$\eqalign{ & \frac{h}{\alpha } = \frac{k}{{\frac{{4\alpha - 20}}{5}}} = \frac{{{h^2} + {k^2}}}{9} \cr & \Rightarrow 5k\alpha = 4h\alpha - 20h{\text{ and }}9h = \alpha \left( {{h^2} + {k^2}} \right) \cr & \Rightarrow \alpha = \frac{{20h}}{{4h - 5k}}{\text{ and }}\alpha = \frac{{9h}}{{{h^2} + {k^2}}} \cr & \Rightarrow \frac{{20h}}{{4h - 5k}} = \frac{{9h}}{{{h^2} + {k^2}}} \cr & \Rightarrow 20\left( {{h^2} + {k^2}} \right) = 9\left( {4h - 5k} \right) \cr} $$
$$\therefore $$ Locus of $$\left( {h,\,k} \right)$$
$$20\left( {{x^2} + {y^2}} \right) - 36x + 45y = 0$$