Question
The locus of the mid-point of a chord of the circle $${x^2} + {y^2} = 4$$ which subtends a right angle at the origin is-
A.
$$x + y = 2$$
B.
$${x^2} + {y^2} = 1$$
C.
$${x^2} + {y^2} = 2$$
D.
$$x + y = 1$$
Answer :
$${x^2} + {y^2} = 2$$
Solution :
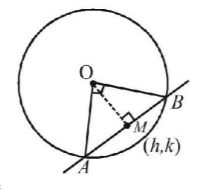
Let $$AB$$ be the chord with its mid point $$M\left( {h,\,k} \right).$$
As $$\angle AOB = {90^ \circ }$$
$$\eqalign{ & \therefore AB = \sqrt {{2^2} + {2^2}} = 2\sqrt 2 \cr & \therefore AM = \sqrt 2 \cr} $$
NOTE THIS STEP
By prop. of rt. $$\Delta $$
$$\eqalign{ & AM = MB = OM \cr & \therefore OM = \sqrt 2 \Rightarrow {h^2} + {k^2} = 2 \cr & \therefore {\text{locus of }}\left( {h,k} \right){\text{ is }}{x^2} + {y^2} = 2 \cr} $$

Let $$AB$$ be the chord with its mid point $$M\left( {h,\,k} \right).$$
As $$\angle AOB = {90^ \circ }$$
$$\eqalign{ & \therefore AB = \sqrt {{2^2} + {2^2}} = 2\sqrt 2 \cr & \therefore AM = \sqrt 2 \cr} $$
NOTE THIS STEP
By prop. of rt. $$\Delta $$
$$\eqalign{ & AM = MB = OM \cr & \therefore OM = \sqrt 2 \Rightarrow {h^2} + {k^2} = 2 \cr & \therefore {\text{locus of }}\left( {h,k} \right){\text{ is }}{x^2} + {y^2} = 2 \cr} $$