Question
The image of the line $$\frac{{x - 1}}{3} = \frac{{y - 3}}{1} = \frac{{z - 4}}{{ - 5}}$$ in the plane $$2x-y+z+3=0$$ is the line :
A.
$$\frac{{x - 3}}{3} = \frac{{y + 5}}{1} = \frac{{z - 2}}{{ - 5}}$$
B.
$$\frac{{x - 3}}{{ - 3}} = \frac{{y + 5}}{{ - 1}} = \frac{{z - 2}}{5}$$
C.
$$\frac{{x + 3}}{3} = \frac{{y - 5}}{1} = \frac{{z - 2}}{{ - 5}}$$
D.
$$\frac{{x + 3}}{{ - 3}} = \frac{{y - 5}}{{ - 1}} = \frac{{z + 2}}{5}$$
Answer :
$$\frac{{x + 3}}{3} = \frac{{y - 5}}{1} = \frac{{z - 2}}{{ - 5}}$$
Solution :
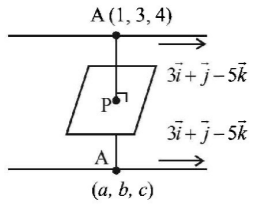
$$\eqalign{ & \frac{{a - 1}}{2} = \frac{{b - 3}}{{ - 1}} = \frac{{c - 4}}{1} = \lambda \,\,\left( {{\text{let}}} \right) \cr & \Rightarrow a = 2\lambda + 1 \cr & b = 3 - \lambda \cr & c = 4 + \lambda \cr & P = \left( {\frac{{a + 1}}{2},\,\frac{{b + 3}}{2},\,\frac{{c + 4}}{2}} \right) \cr & = \left( {\lambda + 1,\,\frac{{6 - \lambda }}{2},\,\frac{{\lambda + 8}}{2}} \right) \cr & \therefore 2\left( {\lambda + 1} \right) - \frac{{6 - \lambda }}{2} + \frac{{\lambda + 8}}{2} + 3 = 0 \cr & \Rightarrow 3\lambda + 6 = 0\,\,\,\,\,\, \Rightarrow \lambda = - 2 \cr & a = - 3,\,\,\,b = 5,\,\,\,c = 2 \cr} $$
Required line is $$\frac{{x + 3}}{3} = \frac{{y - 5}}{1} = \frac{{z - 2}}{{ - 5}}$$

$$\eqalign{ & \frac{{a - 1}}{2} = \frac{{b - 3}}{{ - 1}} = \frac{{c - 4}}{1} = \lambda \,\,\left( {{\text{let}}} \right) \cr & \Rightarrow a = 2\lambda + 1 \cr & b = 3 - \lambda \cr & c = 4 + \lambda \cr & P = \left( {\frac{{a + 1}}{2},\,\frac{{b + 3}}{2},\,\frac{{c + 4}}{2}} \right) \cr & = \left( {\lambda + 1,\,\frac{{6 - \lambda }}{2},\,\frac{{\lambda + 8}}{2}} \right) \cr & \therefore 2\left( {\lambda + 1} \right) - \frac{{6 - \lambda }}{2} + \frac{{\lambda + 8}}{2} + 3 = 0 \cr & \Rightarrow 3\lambda + 6 = 0\,\,\,\,\,\, \Rightarrow \lambda = - 2 \cr & a = - 3,\,\,\,b = 5,\,\,\,c = 2 \cr} $$
Required line is $$\frac{{x + 3}}{3} = \frac{{y - 5}}{1} = \frac{{z - 2}}{{ - 5}}$$