Question
The equation of the incircle of the triangle formed by the axes and the line $$4x + 3y = 6$$ is :
A.
$${x^2} + {y^2} - 6x - 6y + 9 = 0$$
B.
$$4\left( {{x^2} + {y^2} - x - y} \right) + 1 = 0$$
C.
$$4\left( {{x^2} + {y^2} + x + y} \right) + 1 = 0$$
D.
none of these
Answer :
$$4\left( {{x^2} + {y^2} - x - y} \right) + 1 = 0$$
Solution :
If the inradius $$=r$$ then the centre $$ = \left( {r,\,r} \right)$$ and its distance from the line $$4x + 3y = 6$$ is $$r.$$
$$\eqalign{ & {\text{So, }}\left| {\frac{{4r + 3r - 6}}{{\sqrt {{4^2} + {3^2}} }}} \right| = r{\text{ or }}\left| {7r - 6} \right| = 5r \cr & \therefore 7r - 6 = \pm 5r\,\,\,\,\, \Rightarrow r = 3,\,\frac{1}{2} \cr} $$
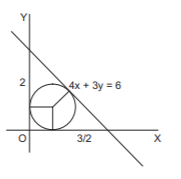
Clearly from the figure, $$r \ne 3$$
$$\therefore $$ the equation of the incircle is $${\left( {x - \frac{1}{2}} \right)^2} + {\left( {y - \frac{1}{2}} \right)^2} = {\left( {\frac{1}{2}} \right)^2}$$
If the inradius $$=r$$ then the centre $$ = \left( {r,\,r} \right)$$ and its distance from the line $$4x + 3y = 6$$ is $$r.$$
$$\eqalign{ & {\text{So, }}\left| {\frac{{4r + 3r - 6}}{{\sqrt {{4^2} + {3^2}} }}} \right| = r{\text{ or }}\left| {7r - 6} \right| = 5r \cr & \therefore 7r - 6 = \pm 5r\,\,\,\,\, \Rightarrow r = 3,\,\frac{1}{2} \cr} $$

Clearly from the figure, $$r \ne 3$$
$$\therefore $$ the equation of the incircle is $${\left( {x - \frac{1}{2}} \right)^2} + {\left( {y - \frac{1}{2}} \right)^2} = {\left( {\frac{1}{2}} \right)^2}$$