Question
The equation of the ellipse with its centre at $$\left( {1,\,2} \right),$$ focus at $$\left( {6,\,2} \right)$$ and passing through the point $$\left( {4,\,6} \right)$$ is $$\frac{{{{\left( {x - 1} \right)}^2}}}{{{a^2}}} + \frac{{{{\left( {y - 2} \right)}^2}}}{{{b^2}}} = 1,$$ then :
A.
$${a^2} = 1,\,{b^2} = 25$$
B.
$${a^2} = 25,\,{b^2} = 20$$
C.
$${a^2} = 20,\,{b^2} = 25$$
D.
None of these
Answer :
None of these
Solution :
Centre is $$\left( {1,\,2} \right)$$ and focus is $$\left( {6,\,2} \right),$$ hence the line joining the centre $$C$$ and the focus $$S$$ (i.e., the axis) is parallel to $$x$$-axis. Therefore, the equation must be of the form
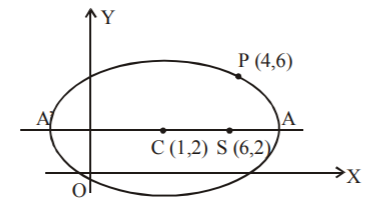
$$\frac{{{{\left( {x - 1} \right)}^2}}}{{{a^2}}} + \frac{{{{\left( {y - 2} \right)}^2}}}{{{b^2}}} = 1......\left( {\text{i}} \right)$$
The distance between the centre and the focus
$$CS = ae = 6 - 1 = 5$$
Also
$${b^2} = {a^2}\left( {1 - {e^2}} \right) = {a^2} - {a^2}{e^2} = {a^2} - 25$$
$$\therefore $$ The equation $$\left( {\text{i}} \right)$$ becomes
$$\frac{{{{\left( {x - 1} \right)}^2}}}{{{a^2}}} + \frac{{{{\left( {y - 2} \right)}^2}}}{{{a^2} - 25}} = 1......\left( {{\text{ii}}} \right)$$
The point $$\left( {4,\,6} \right)$$ lies on it, therefore
$$\eqalign{ & \frac{{{{\left( {4 - 1} \right)}^2}}}{{{a^2}}} + \frac{{{{\left( {6 - 2} \right)}^2}}}{{{a^2} - 25}} = 1\, \Rightarrow {a^2} = 45 \cr & \therefore \,{b^2} = 45 - 25 = 20 \cr} $$
The required equation is $$\frac{{{{\left( {x - 1} \right)}^2}}}{{45}} + \frac{{{{\left( {y - 2} \right)}^2}}}{{20}} = 1$$

$$\eqalign{ & 9ac - 9{a^2} - 2{c^2} > 9ac - 6{c^2}......\left( {\text{i}} \right) \cr & {\text{Again }}3a < 2c \cr & \Rightarrow 9ac < 6{c^2} \cr & \Rightarrow 9ac - 6{c^2}......\left( {{\text{ii}}} \right) \cr & {\text{From }}\left( {\text{i}} \right){\text{and}}\left( {{\text{ii}}} \right),\,\,9ac - 9{a^2} - 2{c^2} > 0 \cr} $$
Centre is $$\left( {1,\,2} \right)$$ and focus is $$\left( {6,\,2} \right),$$ hence the line joining the centre $$C$$ and the focus $$S$$ (i.e., the axis) is parallel to $$x$$-axis. Therefore, the equation must be of the form

$$\frac{{{{\left( {x - 1} \right)}^2}}}{{{a^2}}} + \frac{{{{\left( {y - 2} \right)}^2}}}{{{b^2}}} = 1......\left( {\text{i}} \right)$$
The distance between the centre and the focus
$$CS = ae = 6 - 1 = 5$$
Also
$${b^2} = {a^2}\left( {1 - {e^2}} \right) = {a^2} - {a^2}{e^2} = {a^2} - 25$$
$$\therefore $$ The equation $$\left( {\text{i}} \right)$$ becomes
$$\frac{{{{\left( {x - 1} \right)}^2}}}{{{a^2}}} + \frac{{{{\left( {y - 2} \right)}^2}}}{{{a^2} - 25}} = 1......\left( {{\text{ii}}} \right)$$
The point $$\left( {4,\,6} \right)$$ lies on it, therefore
$$\eqalign{ & \frac{{{{\left( {4 - 1} \right)}^2}}}{{{a^2}}} + \frac{{{{\left( {6 - 2} \right)}^2}}}{{{a^2} - 25}} = 1\, \Rightarrow {a^2} = 45 \cr & \therefore \,{b^2} = 45 - 25 = 20 \cr} $$
The required equation is $$\frac{{{{\left( {x - 1} \right)}^2}}}{{45}} + \frac{{{{\left( {y - 2} \right)}^2}}}{{20}} = 1$$

$$\eqalign{ & 9ac - 9{a^2} - 2{c^2} > 9ac - 6{c^2}......\left( {\text{i}} \right) \cr & {\text{Again }}3a < 2c \cr & \Rightarrow 9ac < 6{c^2} \cr & \Rightarrow 9ac - 6{c^2}......\left( {{\text{ii}}} \right) \cr & {\text{From }}\left( {\text{i}} \right){\text{and}}\left( {{\text{ii}}} \right),\,\,9ac - 9{a^2} - 2{c^2} > 0 \cr} $$