Question
The distance of the point $$\left( {1,\, - 5,\,9} \right)$$ from the plane $$x-y+ z=5$$ measured along the line $$x=y=z$$ is :
A.
$$\frac{{10}}{{\sqrt 3 }}$$
B.
$$\frac{{20}}{3}$$
C.
$$3\sqrt {10} $$
D.
$$10\sqrt {3} $$
Answer :
$$10\sqrt {3} $$
Solution :
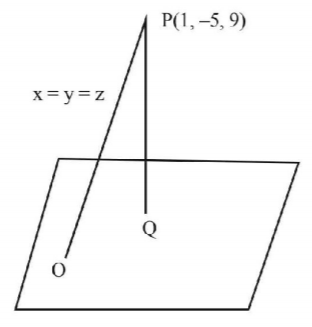
$$\eqalign{ & {\text{Equation of PO :}}\,\,\frac{{x - 1}}{1} = \frac{{y + 5}}{1} = \frac{{z - 9}}{1} = \lambda \cr & \Rightarrow x = \lambda + 1\,;\,\,y = \lambda - 5\,;\,\,z = \lambda + 9 \cr} $$
Putting these in equation of plane :-
$$\eqalign{ & \lambda + 1 - \lambda + 5 + \lambda + 9 = 5 \cr & \Rightarrow \lambda = - 10 \cr & \Rightarrow {\text{O is }}\left( { - 9,\, - 15,\, - 1} \right) \cr & \Rightarrow {\text{distance OP }} = 10\sqrt 3 \cr} $$

$$\eqalign{ & {\text{Equation of PO :}}\,\,\frac{{x - 1}}{1} = \frac{{y + 5}}{1} = \frac{{z - 9}}{1} = \lambda \cr & \Rightarrow x = \lambda + 1\,;\,\,y = \lambda - 5\,;\,\,z = \lambda + 9 \cr} $$
Putting these in equation of plane :-
$$\eqalign{ & \lambda + 1 - \lambda + 5 + \lambda + 9 = 5 \cr & \Rightarrow \lambda = - 10 \cr & \Rightarrow {\text{O is }}\left( { - 9,\, - 15,\, - 1} \right) \cr & \Rightarrow {\text{distance OP }} = 10\sqrt 3 \cr} $$