Question
The components of a vector $$\overrightarrow a $$ along and perpendicular to a non-zero vector $$\overrightarrow b $$ are :
A.
$$\left( {\frac{{\overrightarrow a .\overrightarrow b }}{{{{\left| {\vec b} \right|}^2}}}} \right)\overrightarrow b \& \overrightarrow a - \left( {\frac{{\overrightarrow a .\overrightarrow b }}{{{{\left| {\vec b} \right|}^2}}}} \right)\overrightarrow b $$
B.
$$\left( {\frac{{\overrightarrow a .\overrightarrow b }}{{{{\left| {\overrightarrow a } \right|}^2}}}} \right)\overrightarrow b \& \overrightarrow a + \left( {\frac{{\overrightarrow a .\overrightarrow b }}{{{{\left| {\overrightarrow a } \right|}^2}}}} \right)\overrightarrow b $$
C.
$$\left( {\frac{{\overrightarrow a .\overrightarrow b }}{{{{\left| {\overrightarrow a } \right|}^2}}}} \right)\overrightarrow a - \left( {\frac{{\overrightarrow a .\overrightarrow b }}{{{{\left| {\vec b} \right|}^2}}}} \right)\overrightarrow a $$
D.
None of these
Answer :
$$\left( {\frac{{\overrightarrow a .\overrightarrow b }}{{{{\left| {\vec b} \right|}^2}}}} \right)\overrightarrow b \& \overrightarrow a - \left( {\frac{{\overrightarrow a .\overrightarrow b }}{{{{\left| {\vec b} \right|}^2}}}} \right)\overrightarrow b $$
Solution :
$$\overrightarrow {OM} = $$ component of $$\overrightarrow a $$ along $$\overrightarrow b $$
$$\overrightarrow {MA} = $$ component of $$\overrightarrow a $$ perpendicular to $$\overrightarrow b $$
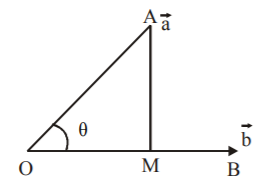
$$\eqalign{ & \Delta OMA \Rightarrow \cos \,\theta = \frac{{OM}}{{OA}} \cr & \Rightarrow OM = \left| {\overrightarrow {OM} } \right| = \left| {\overrightarrow {OA} } \right|\cos \,\theta = \left| {\overrightarrow a } \right|\cos \,\theta \cr & \because \overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|\left| {\overrightarrow b } \right|\cos \,\theta = \left| {\overrightarrow b } \right|\left( {OM} \right) \cr & \therefore \,\overrightarrow {OM} = \left| {\overrightarrow {OM} } \right|\hat b = \left( {\frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\vec b} \right|}}} \right)\frac{{\overrightarrow b }}{{\left| {\vec b} \right|}} = \left( {\frac{{\overrightarrow a .\overrightarrow b }}{{{{\left| {\vec b} \right|}^2}}}} \right)\overrightarrow b \cr & \overrightarrow {OM} + \overrightarrow {MA} = \overrightarrow {OA} \cr & \therefore \,\overrightarrow {MA} = \overrightarrow {OA} - \overrightarrow {OM} = \overrightarrow a - \left( {\frac{{\overrightarrow a .\overrightarrow b }}{{{{\left| {\vec b} \right|}^2}}}} \right)\overrightarrow b \cr} $$
$$\overrightarrow {OM} = $$ component of $$\overrightarrow a $$ along $$\overrightarrow b $$
$$\overrightarrow {MA} = $$ component of $$\overrightarrow a $$ perpendicular to $$\overrightarrow b $$

$$\eqalign{ & \Delta OMA \Rightarrow \cos \,\theta = \frac{{OM}}{{OA}} \cr & \Rightarrow OM = \left| {\overrightarrow {OM} } \right| = \left| {\overrightarrow {OA} } \right|\cos \,\theta = \left| {\overrightarrow a } \right|\cos \,\theta \cr & \because \overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|\left| {\overrightarrow b } \right|\cos \,\theta = \left| {\overrightarrow b } \right|\left( {OM} \right) \cr & \therefore \,\overrightarrow {OM} = \left| {\overrightarrow {OM} } \right|\hat b = \left( {\frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\vec b} \right|}}} \right)\frac{{\overrightarrow b }}{{\left| {\vec b} \right|}} = \left( {\frac{{\overrightarrow a .\overrightarrow b }}{{{{\left| {\vec b} \right|}^2}}}} \right)\overrightarrow b \cr & \overrightarrow {OM} + \overrightarrow {MA} = \overrightarrow {OA} \cr & \therefore \,\overrightarrow {MA} = \overrightarrow {OA} - \overrightarrow {OM} = \overrightarrow a - \left( {\frac{{\overrightarrow a .\overrightarrow b }}{{{{\left| {\vec b} \right|}^2}}}} \right)\overrightarrow b \cr} $$