The common tangents to the circle $${x^2} + {y^2} = 2$$   and the parabola $${y^2} = 8x$$   touch the circle at the points $$P, \,Q$$  and the parabola at the points $$R,\,S.$$  Then the area of the quadrilateral $$PQRS$$   is-

Solution :

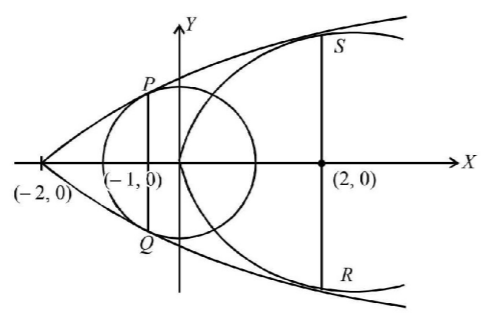
Let the tangent to $${y^2} = 8x$$   be $$y = mx + \frac{2}{m}$$
If it is common tangent to parabola and circle, then $$y = mx + \frac{2}{m}$$   is a tangent to $${x^2} + {y^2} = 2$$
$$\eqalign{ & \therefore \left| {\frac{{\frac{2}{m}}}{{\sqrt {{m^2} + 1} }}} \right| = \sqrt 2 \cr & \Rightarrow \frac{4}{{{m^2}\left( {1 + {m^2}} \right)}} = 2 \cr & \Rightarrow {m^4} + {m^2} - 2 = 0 \cr & \Rightarrow \left( {{m^2} + 2} \right)\left( {{m^2} - 1} \right) = 0 \cr & \Rightarrow m = 1\,\,\,{\text{or }} - 1 \cr} $$
$$\therefore $$ Required tangents are $$y=x+2$$   and $$y=-x-2$$
Their common point is $$\left( { - 2,\,0} \right)$$
$$\therefore $$ Tangents are drawn from $$\left( { - 2,\,0} \right)$$
$$\therefore $$ Chord of contact $$PQ$$  to circle is
$$x.\left( { - 2} \right) + y.0 = 2{\text{ or }}x = - 1$$
and Chord of contact $$RS$$  to parabola is
$$y.0 = 4\left( {x - 2} \right){\text{ or }}x = 2$$
Hence coordinates of $$P$$ and $$Q$$ are $$\left( { - 1,\,1} \right){\text{ and }}\left( { - 1,\, - 1} \right)$$
Also coordinates of $$R$$ and $$S$$ are $$\left( {2,\, - 4} \right){\text{ and }}\left( {2,\,4} \right)$$
$$\therefore $$ Area of trapezium $$PQRS$$   is $$\frac{1}{2}\left( {2 + 8} \right) \times 3 = 15$$