Question
The common chord of $${x^2} + {y^2} - 4x - 4y = 0$$ and $${x^2} + {y^2} = 16$$ subtends at the origin an angle equal to :
A.
$$\frac{\pi }{6}$$
B.
$$\frac{\pi }{4}$$
C.
$$\frac{\pi }{3}$$
D.
$$\frac{\pi }{2}$$
Answer :
$$\frac{\pi }{2}$$
Solution :
The centre of two circles are $${C_1}\left( {2,\,2} \right)$$ and $${C_2}\left( {0,\,0} \right).$$ The radii of two circles are $${r_1} = 2\sqrt 2 $$ and $${r_2} = 4$$
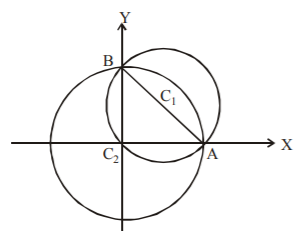
The equation of the common chord of the circles $${x^2} + {y^2} - 4x - 4y = 0$$ and $${x^2} + {y^2} = 16$$ is $$x + y = 4$$ which meets the circle $${x^2} + {y^2} = 16$$ at points $$A\left( {4,\,0} \right)$$ and $$B\left( {0,\,4} \right).$$ Obviously $$OA \bot OB.$$ Hence, the common chord $$AB$$ makes a right angle at the centre of the circle $${x^2} + {y^2} = 16.$$ Where, $$O$$ is the origin and the centre $${C_2}$$ of the second circle.
The centre of two circles are $${C_1}\left( {2,\,2} \right)$$ and $${C_2}\left( {0,\,0} \right).$$ The radii of two circles are $${r_1} = 2\sqrt 2 $$ and $${r_2} = 4$$

The equation of the common chord of the circles $${x^2} + {y^2} - 4x - 4y = 0$$ and $${x^2} + {y^2} = 16$$ is $$x + y = 4$$ which meets the circle $${x^2} + {y^2} = 16$$ at points $$A\left( {4,\,0} \right)$$ and $$B\left( {0,\,4} \right).$$ Obviously $$OA \bot OB.$$ Hence, the common chord $$AB$$ makes a right angle at the centre of the circle $${x^2} + {y^2} = 16.$$ Where, $$O$$ is the origin and the centre $${C_2}$$ of the second circle.