Question
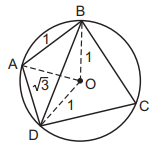
The area of a cyclic quadrilateral $$ABCD$$ is $$\frac{{\left( {3\sqrt 3 } \right)}}{4}.$$ The radius of the circle circumscribing it is $$1.$$ If $$AB = 1,BD = \sqrt 3 $$ then $$BC \cdot CD$$ is equal to
A.
$$2$$
B.
$$3 - \frac{1}{{\sqrt 3 }}$$
C.
$$3\sqrt 3 + 1$$
D.
None of these
Answer :
$$2$$
Solution :
Clearly, $$\angle BOD = 2C$$
$$\eqalign{ & \therefore \,\,\cos 2C = \frac{{{1^2} + {1^2} - {{\left( {\sqrt 3 } \right)}^2}}}{{2 \cdot 1 \cdot 1}}\,\,{\text{or, }}\cos 2C = - \frac{1}{2} \cr & \therefore \,\,C = {60^ \circ } \cr & \therefore \,\,A = {180^ \circ } - C = {120^ \circ }. \cr} $$
So, $$\cos{120^ \circ } = \frac{{A{D^2} + {1^2} - {{\left( {\sqrt 3 } \right)}^2}}}{{2 \cdot AD \cdot 1}}$$
$$\eqalign{ & \therefore \,\, - \frac{1}{2} = \frac{{A{D^2} - 2}}{{2AD}}\,\,{\text{or, }}A{D^2} + AD - 2 = 0 \cr & {\text{or, }}AD = 1. \cr} $$
Now, $${\text{ar}}\left( {ABCD} \right) = {\text{ar}}\left( {\vartriangle ADB} \right) + {\text{ar}}\left( {\vartriangle BCD} \right)$$
or, $$\frac{{3\sqrt 3 }}{4} = \frac{1}{2} \cdot 1 \cdot 1 \cdot \sin {120^ \circ } + \frac{1}{2} \cdot BC \cdot CD \cdot \sin {60^ \circ }\,\,{\text{or, }}BC \cdot CD = 2.$$
Clearly, $$\angle BOD = 2C$$
$$\eqalign{ & \therefore \,\,\cos 2C = \frac{{{1^2} + {1^2} - {{\left( {\sqrt 3 } \right)}^2}}}{{2 \cdot 1 \cdot 1}}\,\,{\text{or, }}\cos 2C = - \frac{1}{2} \cr & \therefore \,\,C = {60^ \circ } \cr & \therefore \,\,A = {180^ \circ } - C = {120^ \circ }. \cr} $$

So, $$\cos{120^ \circ } = \frac{{A{D^2} + {1^2} - {{\left( {\sqrt 3 } \right)}^2}}}{{2 \cdot AD \cdot 1}}$$
$$\eqalign{ & \therefore \,\, - \frac{1}{2} = \frac{{A{D^2} - 2}}{{2AD}}\,\,{\text{or, }}A{D^2} + AD - 2 = 0 \cr & {\text{or, }}AD = 1. \cr} $$
Now, $${\text{ar}}\left( {ABCD} \right) = {\text{ar}}\left( {\vartriangle ADB} \right) + {\text{ar}}\left( {\vartriangle BCD} \right)$$
or, $$\frac{{3\sqrt 3 }}{4} = \frac{1}{2} \cdot 1 \cdot 1 \cdot \sin {120^ \circ } + \frac{1}{2} \cdot BC \cdot CD \cdot \sin {60^ \circ }\,\,{\text{or, }}BC \cdot CD = 2.$$