Question
The area (in sq. units) of the region described by $$\left\{ {\left( {x,\,y} \right):{y^2} \leqslant 2x\,\,{\text{and}}\,y \geqslant 4x - 1} \right\}$$ is-
A.
$$\frac{{15}}{{64}}$$
B.
$$\frac{{9}}{{32}}$$
C.
$$\frac{{7}}{{32}}$$
D.
$$\frac{{5}}{{64}}$$
Answer :
$$\frac{{9}}{{32}}$$
Solution :
Required area
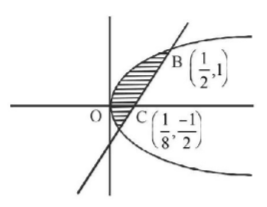
$$\eqalign{ & = {\text{Area of ABCD}} - {\text{ar (ABOCD)}} \cr & = \int\limits_{ - \frac{1}{2}}^1 {\frac{{y + 1}}{4}dy} - \int\limits_{ - \frac{1}{2}}^1 {\frac{{{y^2}}}{2}dy} \cr & = \frac{1}{4}\left[ {\frac{{{y^2}}}{2} + y} \right]_{ - \frac{1}{2}}^1 - \frac{1}{2}\left[ {\frac{{{y^3}}}{2}} \right]_{ - \frac{1}{2}}^1 \cr & = \frac{1}{4}\left[ {\frac{3}{2} + \frac{3}{8}} \right] - \frac{9}{{48}} \cr & = \frac{{15}}{{32}} - \frac{9}{{48}} \cr & = \frac{{27}}{{96}} \cr & = \frac{9}{{32}} \cr} $$
Required area

$$\eqalign{ & = {\text{Area of ABCD}} - {\text{ar (ABOCD)}} \cr & = \int\limits_{ - \frac{1}{2}}^1 {\frac{{y + 1}}{4}dy} - \int\limits_{ - \frac{1}{2}}^1 {\frac{{{y^2}}}{2}dy} \cr & = \frac{1}{4}\left[ {\frac{{{y^2}}}{2} + y} \right]_{ - \frac{1}{2}}^1 - \frac{1}{2}\left[ {\frac{{{y^3}}}{2}} \right]_{ - \frac{1}{2}}^1 \cr & = \frac{1}{4}\left[ {\frac{3}{2} + \frac{3}{8}} \right] - \frac{9}{{48}} \cr & = \frac{{15}}{{32}} - \frac{9}{{48}} \cr & = \frac{{27}}{{96}} \cr & = \frac{9}{{32}} \cr} $$