Question
The area enclosed between the curves $$y = a{x^2}$$ and $$x = a{y^2}\left( {a > 0} \right)$$ is $$1$$ sq. unit, then the value of $$a$$ is :
A.
$$\frac{1}{{\sqrt 3 }}$$
B.
$$\frac{1}{2}$$
C.
$$1$$
D.
$$\frac{1}{3}$$
Answer :
$$\frac{1}{{\sqrt 3 }}$$
Solution :
$$y = a{x^2}\,\& \,x = a{y^2}$$
Points of intersection are $$O\left( {0,\,0} \right)\,\& \,A\left( {\frac{1}{a},\,\frac{1}{a}} \right)$$
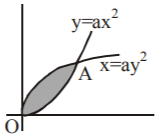
$$\eqalign{ & \therefore \,{\text{Area}} = \int\limits_0^{\frac{1}{a}} {\left( {\sqrt {\frac{x}{a}} - a{x^2}} \right)} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \,\frac{2}{{3{a^2}}} - \frac{1}{{3{a^2}}} = \frac{1}{{3{a^2}}} = 1 \cr & \Rightarrow a = \frac{1}{{\sqrt 3 }} \cr} $$
$$y = a{x^2}\,\& \,x = a{y^2}$$
Points of intersection are $$O\left( {0,\,0} \right)\,\& \,A\left( {\frac{1}{a},\,\frac{1}{a}} \right)$$
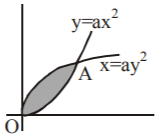
$$\eqalign{ & \therefore \,{\text{Area}} = \int\limits_0^{\frac{1}{a}} {\left( {\sqrt {\frac{x}{a}} - a{x^2}} \right)} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \,\frac{2}{{3{a^2}}} - \frac{1}{{3{a^2}}} = \frac{1}{{3{a^2}}} = 1 \cr & \Rightarrow a = \frac{1}{{\sqrt 3 }} \cr} $$