Question
The area enclosed between the curves $${y^2} = x$$ and $$y = \left| x \right|$$ is-
A.
$$\frac{1}{6}$$
B.
$$\frac{1}{3}$$
C.
$$\frac{2}{3}$$
D.
$$1$$
Answer :
$$\frac{1}{6}$$
Solution :
The area enclosed between the curves $${y^2} = x$$ and $$y = \left| x \right|$$
From the figure, area lies between $${y^2} = x$$ and $$y=x$$
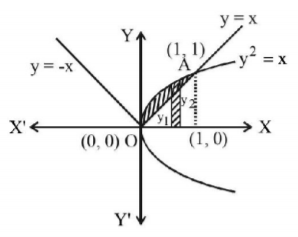
$$\eqalign{ & \therefore {\text{Required area}} = \int_0^1 {\left( {{y_2} - {y_1}} \right)dx} \cr & = \int_0^1 {\left( {\sqrt x - x} \right)dx} \cr & = \left[ {\frac{{{x^{\frac{3}{2}}}}}{{\frac{3}{2}}} - \frac{{{x^2}}}{2}} \right]_0^1 \cr & \therefore {\text{Required area}} = \frac{2}{3}\left[ {{x^{\frac{3}{2}}}} \right]_0^1 - \frac{1}{2}\left[ {{x^2}} \right]_0^1 = \frac{2}{3} - \frac{1}{2} = \frac{1}{6} \cr} $$
The area enclosed between the curves $${y^2} = x$$ and $$y = \left| x \right|$$
From the figure, area lies between $${y^2} = x$$ and $$y=x$$

$$\eqalign{ & \therefore {\text{Required area}} = \int_0^1 {\left( {{y_2} - {y_1}} \right)dx} \cr & = \int_0^1 {\left( {\sqrt x - x} \right)dx} \cr & = \left[ {\frac{{{x^{\frac{3}{2}}}}}{{\frac{3}{2}}} - \frac{{{x^2}}}{2}} \right]_0^1 \cr & \therefore {\text{Required area}} = \frac{2}{3}\left[ {{x^{\frac{3}{2}}}} \right]_0^1 - \frac{1}{2}\left[ {{x^2}} \right]_0^1 = \frac{2}{3} - \frac{1}{2} = \frac{1}{6} \cr} $$