Question
The area bounded by the parabolas $$y = {\left( {x + 1} \right)^2}$$ and $$y = {\left( {x - 1} \right)^2}$$ and the line $$y = \frac{1}{4}$$ is-
A.
$$4\,{\text{sq}}{\text{.}}\,{\text{units}}$$
B.
$$\frac{1}{6} \,{\text{sq}}{\text{.}}\,{\text{units}}$$
C.
$$\frac{4}{3} \,{\text{sq}}{\text{.}}\,{\text{units}}$$
D.
$$\frac{1}{3} \,{\text{sq}}{\text{.}}\,{\text{units}}$$
Answer :
$$\frac{1}{3} \,{\text{sq}}{\text{.}}\,{\text{units}}$$
Solution :
The given curves are
$$y = {\left( {x + 1} \right)^2}.....(1)$$
upward parabola with vertex at $$\left( { - 1,\,0} \right)$$ meeting $$y$$-axis at $$\left( {0,\,1} \right)$$
$$y = {\left( {x - 1} \right)^2}.....(2)$$
upward parabola with vertex at $$\left( {1,\,0} \right)$$ meeting $$y$$-axis at $$\left( {1,\,0} \right)$$
$$y = \frac{1}{4}.....(3)$$
a line parallel to $$x$$-axis meeting (1) at $$\left( { - \frac{1}{2},\,\frac{1}{4}} \right),\,\left( { - \frac{3}{2},\,\frac{1}{4}} \right)$$
and meeting (2) at $$\left( {\frac{3}{2},\,\frac{1}{4}} \right),\left( {\frac{1}{2},\,\frac{1}{4}} \right)$$
The graph is as shown
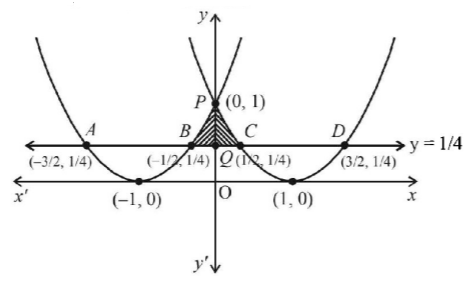
The required area is the shaded portion given by ar $$\left( {BPCQB} \right) = 2Ar\left( {PQCP} \right)$$ (by symmetry)
$$\eqalign{ & = 2\left[ {\int\limits_0^{\frac{1}{2}} {\left( {{{\left( {x - 1} \right)}^2} - \frac{1}{4}} \right)dx} } \right] \cr & = 2\left[ {\left( {\frac{{{{\left( {x - 1} \right)}^3}}}{3} - \frac{x}{4}} \right)_0^{\frac{1}{2}}} \right] \cr & = 2\left[ {\left( { - \frac{1}{{24}} - \frac{1}{8}} \right) - \left( { - \frac{1}{3}} \right)} \right] \cr & = 2\left[ {\frac{{ - 1 - 3 + 8}}{{24}}} \right] \cr & = \frac{1}{3}{\text{ sq}}{\text{. units}} \cr} $$
The given curves are
$$y = {\left( {x + 1} \right)^2}.....(1)$$
upward parabola with vertex at $$\left( { - 1,\,0} \right)$$ meeting $$y$$-axis at $$\left( {0,\,1} \right)$$
$$y = {\left( {x - 1} \right)^2}.....(2)$$
upward parabola with vertex at $$\left( {1,\,0} \right)$$ meeting $$y$$-axis at $$\left( {1,\,0} \right)$$
$$y = \frac{1}{4}.....(3)$$
a line parallel to $$x$$-axis meeting (1) at $$\left( { - \frac{1}{2},\,\frac{1}{4}} \right),\,\left( { - \frac{3}{2},\,\frac{1}{4}} \right)$$
and meeting (2) at $$\left( {\frac{3}{2},\,\frac{1}{4}} \right),\left( {\frac{1}{2},\,\frac{1}{4}} \right)$$
The graph is as shown

The required area is the shaded portion given by ar $$\left( {BPCQB} \right) = 2Ar\left( {PQCP} \right)$$ (by symmetry)
$$\eqalign{ & = 2\left[ {\int\limits_0^{\frac{1}{2}} {\left( {{{\left( {x - 1} \right)}^2} - \frac{1}{4}} \right)dx} } \right] \cr & = 2\left[ {\left( {\frac{{{{\left( {x - 1} \right)}^3}}}{3} - \frac{x}{4}} \right)_0^{\frac{1}{2}}} \right] \cr & = 2\left[ {\left( { - \frac{1}{{24}} - \frac{1}{8}} \right) - \left( { - \frac{1}{3}} \right)} \right] \cr & = 2\left[ {\frac{{ - 1 - 3 + 8}}{{24}}} \right] \cr & = \frac{1}{3}{\text{ sq}}{\text{. units}} \cr} $$