Question
The area bounded by the lines $$y = \left| {x - 2} \right|,\,\left| x \right| = 3$$ and $$y=0$$ is :
A.
$$13{\text{ uni}}{{\text{t}}^2}$$
B.
$$5{\text{ uni}}{{\text{t}}^2}$$
C.
$$9{\text{ uni}}{{\text{t}}^2}$$
D.
$$7{\text{ uni}}{{\text{t}}^2}$$
Answer :
$$13{\text{ uni}}{{\text{t}}^2}$$
Solution :
$${\text{Area}} = \frac{1}{2}.1.1 + \frac{1}{2}.5.5.\frac{{26}}{2} = 13$$
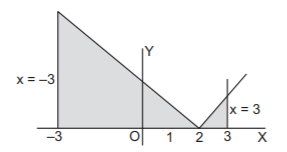
$${\text{Area}} = \frac{1}{2}.1.1 + \frac{1}{2}.5.5.\frac{{26}}{2} = 13$$
